简介
线性表(Linear_List)是一种典型的线性结构结构,它是由n个数据元素(结点)al,a2,...,an组成的有限序列。
特点
对于一个非空的线性表:
- ①有且仅有一个称为开始元素的a,它没有前趋,仅有一个直接后继a2;
- ②有且仅有一个称为终端元素的an,它没有后继,仅有一个直接前趋;
- ③其余元素ai(2≤i≤n-1)称为内部元素,它们都有且仅有一个直接前趋ai-1和一个直接后继ai+1。
线性表中元素之间的逻辑关系就是相邻关系,又称为线性关系
线性表的基本运算
- (1)置空表InitList(L),构造一个空的线性表L。
- (2)求表长ListLength(L),返回线性表L中元素个数,即表长。
- (3)取表中第i个元素GetNode(L, i),若1≤i≤ListLength(L),则返回第i个元素ai。
- (4)按值查找LocatelMlode(L,x),在表L中查找第一个值为x的元素,并返回该元素在表L中的位置,若表中没有元素的值为x,则返回0值。
- (5)插入InsertList(L,i,x),在表L的第i元素之前插入一个值为x的新元素,表L的长度加1。
- (6)删除DeleteList(L, i),册除表L的第i个元素,表L的长度减1。
线性表的顺序存储
顺序表
概念
将线性表的数据元素按其逻辑次序依次存入一组地址连续的存储单元里
存储地址
当顺序表中每个结点占用d(d>1)个存储单元,而且已知起始结点a的存储地址是Loc(a1),则可以通过下列公式求得任一结点ai的存储地址Loc(ai):
Loc (ai) = Loc (a1) +(i-1) *d
特点
元素在表中的相邻关系,在计算机内也存在着相邻的关系。
数据类型定义
#define ListSize 1001 //表的大小根据实际需要定义,这里假设为100
typedef int Datalype; //Datalype的数据类型根据实际情况而定,这里定义为int
typedef struct
{
DataType data[Listsize]; //数组data用来存放表结点
int length; //线性表的当前长度(实际元素的个数)
}SeaqList; //顺序表的数据类型名
内存中表示
SeqList L; //定义变量L为顺序表类型的变量

插入运算
在线性表的第i-1个元素和第i个元素之间插入一个新元素x。
步骤
- ①将结点ai,...., a各后移一位以便腾出第i个位置;
- ②将x置入该空位;
- ③表长加1。此外,必须在上述各步之前判断参数i即插入位置是否合法。

算法描述
void InsertList (SeqLlst *L,int i,DataType x){ //在顺序表L中第i个位置之前插入一个新元素x
int j;
if(i<1 || i> L-> length+1) //判断i值是否合法? 当i<1或i>length+1时,i值不合法。
{
printf("position error");
return;
}
if(L-> length >= ListSize) //判断L是否已满?当L->length>=ListSize时,表示L已满。
{
printf("overflow");
return;
}
for(j = L->length-1 ; j>=i-l ; j--)
L->data[j+1]=L->data[j]; //从最后一个元素开始逐一后移
L->data[i-1]=x; //插入新元素x
L->length++; //实际表长加1
}
删除运算
将表的第i个结点删去,使其长度为变成n-1。
步骤
- ①从ai+1,…,an依次向前移一个位置;
- ②表长减1。

算法描述
DataType DeleteList(SeqLlst *L,int i) { //删除顺序表L中第i个元素
int j; DataType x
if(i<1 || i>L->length) //判断i值是否合法?当i<l或i>length时,i值不合法。
{
printf("position error");
exit(O); //不合法退出
}
DataType x = L->data[i]; //保存被删除的元素
for(j=i ; j<= L->length-1 ; j++) {
L->data[j] = L->data[j + 1]; //元素前移
}
L->length--; //实际表长减1
return x; //返回被删除的元素}
}
线性表的链式存储
单链表
链表不同于顺序表,顺序表占用的存储空间必须是连续的,而链表的各结点占用的存储空间之间可以是连续的,也可以是不连续的,但每一个链结点内部占用的存储单元的地址必须是连续的。因此链表中结点的逻辑次序和物理次序不一定相同,通过指针来反映结点之间的逻辑关系。
结构
[数据域][指针域]

数据类型定义
typedef struct node //结点类型定义
{
DataType data; //结点数据域
struct node *next; //结点指针域
}ListNode;
typedef ListNode *LinkList;
ListNode *p; //定义一个指向结点的指针变量
LinkList head; //定义指向单链表的头指针
单链表建立
动态建立单链表的常用方法有两种:一种是头插法,另一种则是尾插法。
(1)头插法
从一个空表开始,重复读入数据,生成新结点,将读入的数据存放到新结点的数据域中,然后将新结点插入到当前链表的表头上,直到读入结束标志为止。

算法描述
LirkList CreateListF()
{
LinkList head;
ListNode *p;
char ch;
head=NULL; //置空单链表
ch=getchar(); //读入第一个字符
while(ch!='\n') //读入字符不是结束标志符时作循环
{
p=(ListMode *)malloc(sizeof(ListNode)); //分配一个类型为ListNode的结点的地址空间,并将其首地址存入指针变量p中。
p->data=ch; //数据域赋值
p->next=head; //指针域赋值
head=p; //头指针指向新结点
ch=getchar(); //读入下一个字符
}
return head; //返回链表的头指针
}
(2)尾插法
将新结点插入在当前链表的表尾上,因此需要增设一个尾指针rear,使其始终指向链表的尾结点。

算法描述
LinkList CreateListR()
{
LinkList head,rear;
ListNode *p;
char ch;
head=NULL; rear=NULL; //置空单链表
ch=getchar (); //读入第一个字符
while(ch!='in') //读入字符不是结束标志符时作循环
{
p=(ListNode *)malloc(Sizeof(ListNode)); //申请新结点
p->data=ch; //数据域赋值
if(head==NULL)
head=p; //新结点*p插入空表
else
rear->next=p; //新结点*r插入到非空表的表尾结点*rear之后
rear=p; //表尾指针指向新的表尾结点
ch=getchar(); //读入下一个字符
}
if(rear != null)
rear->next = NULL;
return head;
}
带头结点的单链表
可以简化单链表的算法

算法描述
以尾插法
LinkList CreateLlstRl(){ //尾插法建立带头结点的单链表算法
LinkList head=(ListNode*)malloc(Sizeof(ListNode)); //申请头结点
ListNode *p,*r;
DataType ch;
r=head; //尾指针初始指向头结点
while((ch=getchar( ))!='\n')
{
p=(ListNode *)malloc(sizeof(ListNode)); //申请新结点
p->data=ch;
r->next=p; //新结点连接到尾结点之后
r=p; //尾指针指向新结点
}
r->next=NULL; //终端结点指针域置空
return head;
}
查找运算
(1)在单链表中要查找第i个结点
算法描述
ListNode *GetNodei(LinkList head,int i)
{
//head为带头结点的单链表的头指针,i为要查找的结点序号
ListNode *p; int j;
p=head->next; j=1; //使p指向第一个结点,j置1
while(p!=NULL&&j<i) //顺指针向后查找,直到p指向第i个结点或p为空为止
{
p=p->next; ++j;
}
if(j==i) //若查找成功,则返回查找结点的存储地址(位置),否则返回NULL
return p;
else
return NULL;
}
(2)在单链表中查找值为k的结点
算法描述
LiStNode * LocateNodek (LinkList head,DataType k)
{
//head为带头结点的单链表的头指针,k为要查找的结点值
ListNode *p=head->next; //p指向开始结点
while(p&&p->data!=k) //循环直到p等于NULL或p->data等于k为止
p=p->next; //指针指向下一个结点
return p; //若找到值为k的结点,则p指向该结点,否则p为NULL
}
插入运算
将值为x的新结点插入到表的第i个结点的位置上,即插入到ai-1与ai之间。
算法思想
先使p指向ai-1的位置,然后生成一个数据域值为x的新结点*s,再进行插入操作。
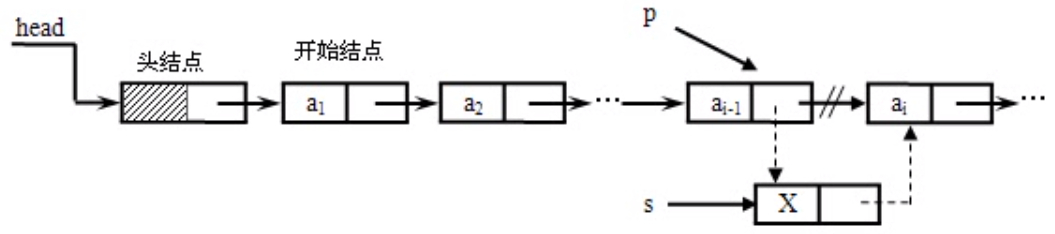
算法描述
void InsertList (LinkList head,int i,DataType X)
{
//在以head为头指针的带头结点的单链表中第i个结点的位置上
//插入一个数据域值为X的新结点
ListNode *p,*s; int j;
p=head; j=0;
while(p!=NULL&j<i-1) //使p指向第i-1个结点
{
p=p->next; ++j;
}
if(p==NULL) //N入位置错误
{
printf("ERRORn");
return;
}
else {
s=(ListNode*)malloc(Sizeof(ListNode)); //申请新结点
s->data=X; s->next=p->next; //进行插入
p->next=s;
}
}
删除运算
将链表的第i个结点从表中删去。
算法思想
先使p指向ai-1的位置,然后执行p->next指向第i+1个结点,再将第i个结点释放掉。

算法描述
DataType DeleteList(LinkList head,int i)
{
//在以head为头指针的带头结点的单链表中删除第i个结点
ListNode *p,*s;
dataType x; int j;
p=head; j=0;
while(p!=NULL&&j<i-1) //使p指向第i-1个结点
{
p=p->next j++;
}
if(p==NULL) //册阶位置错误
{
printf("位置错误\n");
exit(O); //出错退出处理
}
else {
s=p->next; //s指向第i个结点
p->next=s->next; //使p->next指向第i+1个结点
x=s->data; //保存被删除结点的值
free(s); return x; //删除第i个结点,返回结点值
}
}
循环链表
循环链表与单链表的区别仅仅在于其尾结点的链域值不是NULL,而是一个指向头结点的指针。
循环链表的主要优点是:从表中任意一结点出发都能通过后移操作而遍历整个循环链表。
在循环链表中,将头指针改设为尾指针(ream)后,无论是找头结点、开始结点还是终端点都很方便,它们的存储位置分别是rear->next、rear->next->next和rear,这样可以简化某些操作。
头部

尾部

算法描述
例:已知有一个结点数据域外围整型,且按从大到小顺序排列的头结点指针为L的非空单循环链表,试写一算法插入一结点(其数据域为x)至血循环链表适当位置
void InsertList(LinkList L,int x)
{
//将值为x的新结点插入到有序循环链表中适当的位置
ListNode *s,*p,*q;
s=(ListNode *)malloc(sizeof(ListNode)); //申请结点存储空间
s->data=x; p=L;
q=p->next; //q指向开始结点
while(q->data>x&&q!=L) //查找插入位置
{
p=p->next; //p指向q的前趋结点
q=p->next; //q指向当前结点
}
p->next=s; //插入*s结点
s->next=q;
}
双向链表
双链表结构是一种对称结构,既有前向链,又有后向链,这就使得插入操作及删除操作都非常方便。
设指针p指向双链表的某一结点,则双链表结构的对称性可用下式来描述:
p->prior ->next == p->next->prior == p
在双链表上实现求表长、按序号查找、定位、插入和删除等运算与单链表上的实现方法基本相同,不同的主要是插入和删除操作。
结构
[前向链][数据][后向链]


数据类型定义
typedef struct dlnode
{
DataType data;
struct dlnode *prior,*next;
}DLNode; //双向链表结点的类型定义typedef DLNode*DLinkList;
删除操作
删除双链表中p所指结点
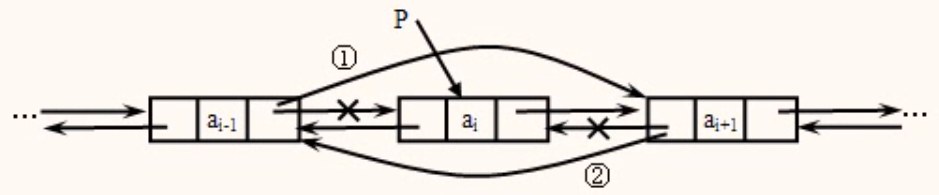
步骤
- ①p ->prior ->next=p->next;
- ②p ->next ->prior=p->prior;
算法描述
DataType DLDelete(DLNode *p)
{
//删除带头结点的双向链表中指定结点*p
p->prior->next=p->next;
p->next->prior=p->prior; //上面两条语句的顺序可以调换,不影响操作结果。
x=p->data;
free(p);
return x;
}
插入操作
将值为x的新结点插入到带头结点的双向链表中指定结点r之前。
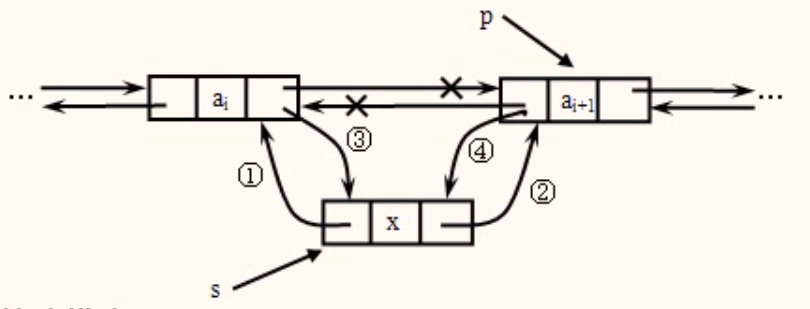
算法描述
void DLInsert(DLNode *p,Datalype x)
{
//将值为x的新结点插入到带头结点的双向链表中指定结点*p之前
DLNode *s=(DLNode* )malloc(sizeof(DLNode)); //申请新结点
s->data=x;
s->prior=p->prior; //完成①步操作
s->next=p; //完成②步操作
p->prior->next=s; //完成③步操作
p->prior=s; //完成④步操作
}
补充
在p所指结点的后面链入一个新结点*s,则需修改四个指针:
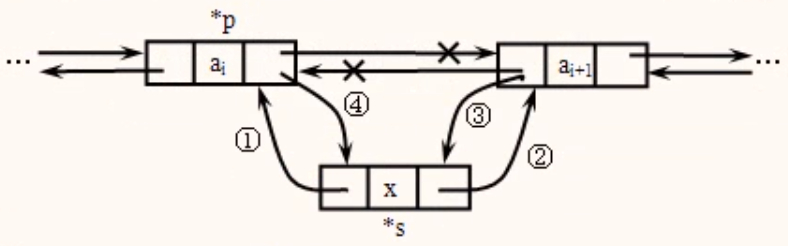
①s->prior= p; ②s->next=p->next;
③p->next->prior=s; ④p->next=s;
注:③和④两条语句的顺序不能调换,否则操作结果错误。下面四条语句也可以完成插入操作。
①s->prior=p; ②s->next=p->next;
③p->next=s; ④s->next->prior=s;
顺序表的优缺点
优点
- ①空间利用率高。
- ②可以实现随机存取。
缺点
- ①插入、删除操作中要大量移动结点,时间性能差。
- ②需要事先确定顺序表的大小,估计小了会发生溢出现象,估计大了又将造成空间的浪费。
链表的优缺点
优点
- ①插入、删除操作中无需移动结点,时间性能好。
- ②因为是动态分配存储空间,所以只要有空闲空间就不会发生溢出现象。
缺点
因为每个结点都要额外设置指针域,因此空间利用率低。
顺序表和链表比较
- ①对线性表的操作是经常性的查找运算,以顺序表形式存储为宜。因为顺序存储可以随机访问任一结点,访问每个结点的复杂度均为O(1)。而链式存储结构必须从表头开始沿链逐一访问各结点,其时间复杂度为0(n)。
- ②如果经常进行的运算是插入和删除运算,以链式存储结构为宜。因为顺序表作插入和删除操作需要移动大量结点,而链式结构只需要修改相应的指针。
- ③对于线性表结点的存储密度问题,也是选择存储结构的一个重要依据。所谓存储密度就是结点空间的利用率。它的计算公式为:存储密度=(结点数据域所占空间)/(整个结点所占空间)。结点存储密度越大,存储空间的利用率就越高。
