死锁的检测与解除
假如系统为进程分配资源时,不采取任何限制性措施来避免和预防死锁,而是在操作系统运行过程中,不断地监督程序的执行和资源占用情况,判断是否发生死锁,一旦发生死锁,采取专门的措施解除死锁,并以最小代价使系统恢复正常。
死锁检测时机
检测的实质:
检测算法检测是否存在“循环等待”条件。
时机
- 一次资源分配后
- 每次调度后
- 定时器定时运行检测程序
- 当某个进程长期处于阻塞状态或阻塞程序过多时
死锁的检测算法
过程
- 为每个进程和每个资源指定唯一编号
- 设置一张资源分配状态表,每个表目包含“资源号”和占有该资源的“进程号”两项,资源分配表中记录每个资源正在被哪个进程所占有
- 设置一张进程等待分配表,每个表目包含“进程号”和该进程所等待的“资源号”两项
算法规则
当任一进程Pj申请一个已被占用的资源Ri时,进行死锁检测,反复查找资源分配表和等待进程表,来确定Pj对资源Ri的请求是否导致形成环路,若是,出现死锁。
如下图
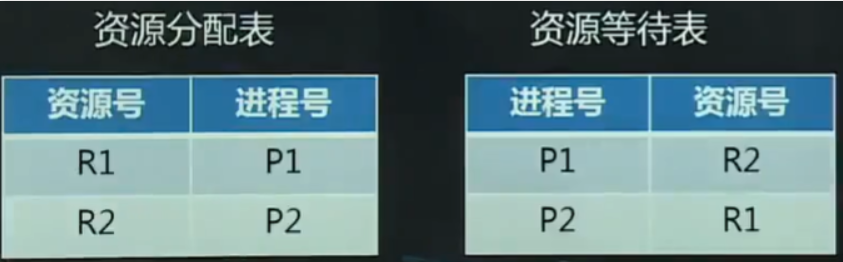
死锁解除算法
- 剥夺资源。一旦死锁,挂起一些进程,剥夺它们占有的资源给死锁进程,以解除死锁。
- 撤销进程。一旦死锁,挂起一些进程,剥夺它们占有的资源给死锁进程,以解除死锁。可以一次撤销所有死锁进程,也可以逐个撤销。
资源分配图SRAG(System Resource Allocation Graph)
资源分配图SRAG(System Resource Allocation Graph)
作用
描述系统中资源分配和申请情况,对死锁进行分析并采取对策
SRAG定义
是一张有向图,可定义为一个二元组,即,SRAG=(V,E),其中V是顶点的集合,包括进程集合、资源集合E是有向边的集合,是一个有序对<Pi,ri>。
V顶点集合
点集合可分为两部分:P = (P1,P2,...,Pn),是由系统内的所有进程组成的集合,每个Pi代表一个进程;R = (r1,r2,...,rm),是系统内所有资源组成的集合,每个ri代表一类资源
E有向边集合
边集E中的每条边是一个有序对<Pi,ri>或<ri,Pi>。Pi进程(Pi∈P),ri是资源类型(ri∈R)。 如果<Pi,ri>∈E ,则存在 一条Pi指向ri的有向边,它表示Pi提出了一个要求分配ri类资源中的一个资源的请求,并且当前正在等待分配。如果<ri,Pi>∈E,则存在一条从ri类资源指向进程Pi的有向边,它表示ri类资源中的某个资源已分配给了进程Pi。有向边<Pi,ri>叫作请求边,而有向边<ri,Pi>则叫作分配边
有向图
在有向图中,用圆圈表示进程,用方框表示每类资源。每类资源ri可能有多个实例。可用方框中的圆点(实心圆点)表示各个资源实例。申请边为从进程到资源的有向边,表示进程申请一个资源,但当前该进程在等待该资源。分配边为从资源到进程的有向边,表示有一个资源实例分配给进程。注意:一条申请边仅指向代表资源类ri的方框,表示申请时不指定哪一个资源实例,而分配边必须由方框中的圆点引出,表示哪一个资源实例已经被占有。
当进程Pi请求资源类ri的一个实例时,将一条请求边加入资源分配图,如果这个请求是可以满足的,则该请求边立即装换成分配边;当进程随后释放了某个资源时,则删除分配边
如图所示:系统资源分配图示例
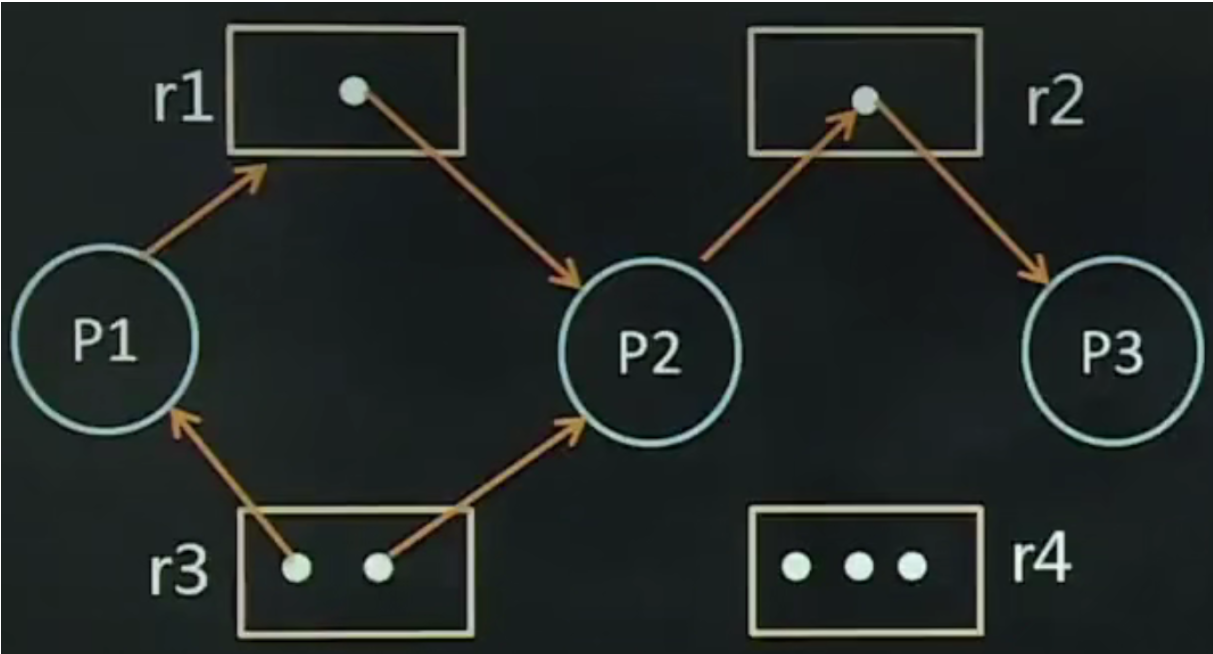
内容详解
集合P,R,E分别为:
P = {P1,P2,P3} R = {r1,r2,r3,r4}
E = {<P1,r1>,<P2,r2>,<r1,P2>,<r2,P3>,<r3,P1>,<r3,P2>}
资源实例个数为:
| r1 | = 1,| r2 | = 1,| r3 | = 2,| r4 | = 3
进程状态如下:
1) 进程P1已经占用一个r3类资源,且正在等待获得一个r1类资源
2) 进程P2已占用r1和r3类资源各一个且正在等待获得一个r2类资源
3) 进程P3已占用一个r2类资源
从上面图可看,资源分配无环路,无死锁
死锁定理
基于上述资源分配图的定义,可给出判定死锁的法则,又称死锁定理
作用
判定死锁的法则
规则如下
- (1)如果资源分配图中没有环路,则系统无死锁
- (2)如果资源分配图中出现了环路,则可能存在死锁
判定条件如下:
- 如果处于环路中的每个资源类中均包含一个资源实例,则环路存在意味着死锁的存在。此时,环路是死锁的充分必要条件。如下图所示
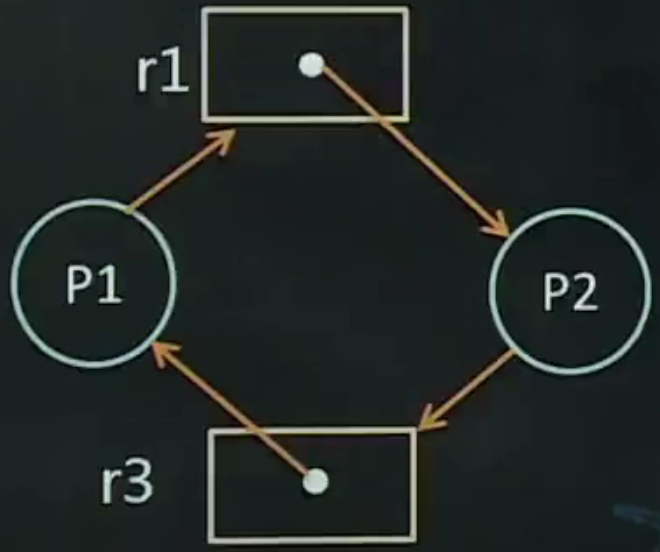
- 如果处于环路中的每个资源类中实例的个数不全为1,则环路存在是死锁的必要条件而非充分条件。如下图
有环路有死锁
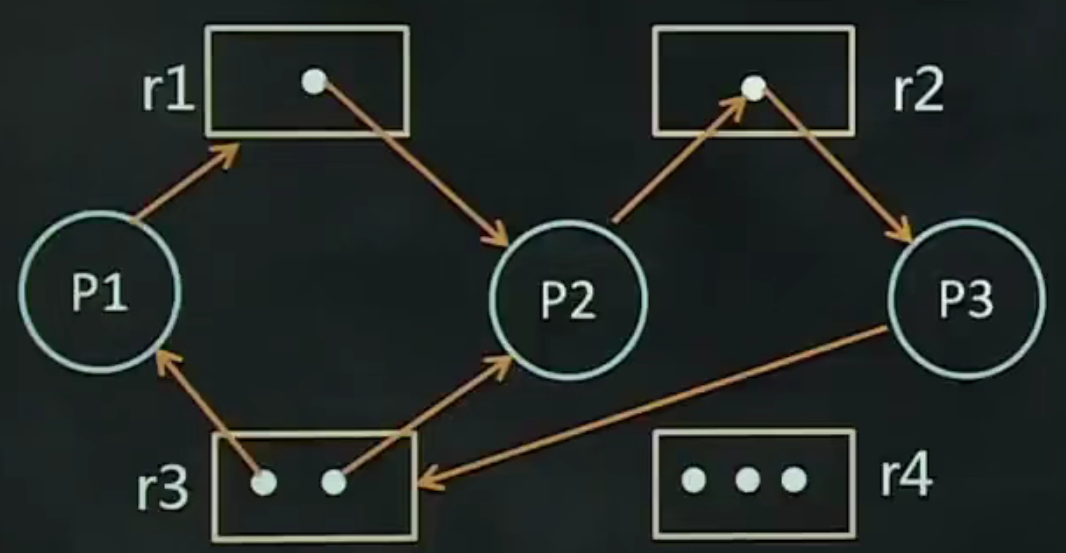
解释:存在两个环路P1->r1->P2->r2->P3-r3->P1,环路P2->r2->P3->r3->P2。P1、P2、P3都陷入了死锁。
有环路但无死锁
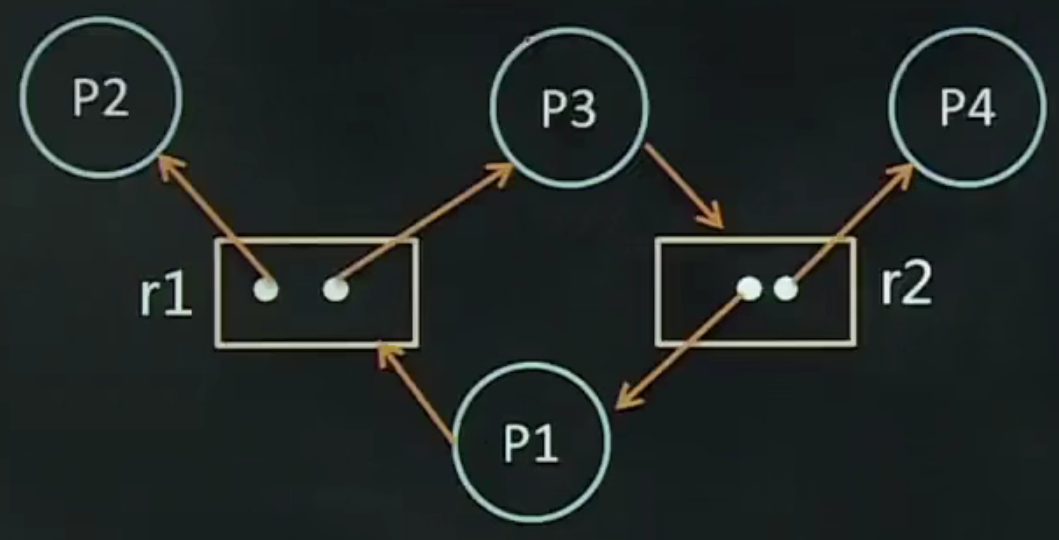
解释:存在环路P1->r1->P3->r2->P1,但无死锁。因为当P4释放了一个r2类资源后,可将它分给P3或者P2释放一个r2类资源后将它分给P1,这两种情况下环路都消失了,因而不会发生死锁
资源分配图化简方法
可以使用资源分配图简化方法,来检测系统是否为死锁状态。
指若一个进程的所有资源请求均能被满足,可以设想该进程得到其所需的全部资源,最终完成任务,运行完毕,并释放所占有的全部资源。则称资源分配图可以被化简。假若一个资源分配图可被其所有进程化简,则称该进程是可化简的,否则不可化简
步骤如下
- (1)在资源分配图中,找出一个既不阻塞又非独立的进程结点Pi。在顺利的情况下,Pi问获得所需资源而继续运行,直至运行完毕,再释放其所占有的全部资源,这相当于消去Pi的请求边和分配边,使之成为孤立的结点。
- (2)将Pi释放的资源分配给申请它的进程,若该进程能顺利运行完,释放资源,再次成为孤立结点。
- (3)重复(1)(2)步,直到找不到符合条件的进程结点。
经过化简后,若能消去所有的边,则该图可完全简化系统不存在死锁;否则不可完全简化,存在死锁。
例子
以上面两图为例
- 1.在有环路有死锁中,找不到任何一个既非等待、又非孤立的进程结点,所以该资源分配图不可化简,所以该系统发生了死锁
- 2.有环路有死锁,可以找到既非等待、又非孤立的进程结点(P1、P2)

化简过程
首先找到既非等待、又非孤立得到P4结点,消去其分配边,得到一个可用资源r2,由于P3有一条r2的申请边,可将该资源分配给P2,即将P2的申请边改为分配边。在得到新的资源分配图中,可以找到既非等待,又非孤立的进程P3,继续将其相应的分配边消去,并将P1对r1的申请边改为分配边(因为P3进程获得结束,释放r1资源),...最终资源分配图中所有进程结点都变成孤立结点,则该资源分配图是可化简的,得出结论,该系统没有发生死锁
哲学家就餐问题
问题描述
有5个哲学家以思考、用餐交替进行的方式生活,他们坐在一张圆桌边,桌子上有5个盘子和5只筷子。如下图所示。当一个哲学家思考时,他与邻座的哲学家没有任何联系。当一个哲学家感到饿了,他就是图拿起他左右两边的筷子用餐。如果他的邻座已经拿到筷子,则他可能只能拿到一只甚至一只筷子也拿不到。当一个饥饿的哲学家得到两根筷子,他就可以用餐。当他用餐完毕,他就放下筷子并再次进行思考
如下图:
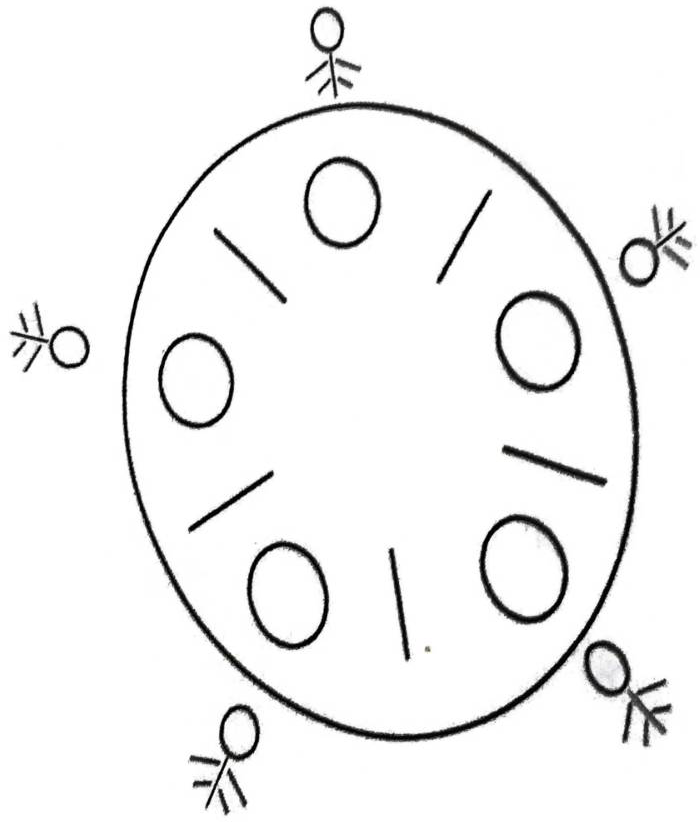
问题精简
- (1)有五个哲学家围坐在一圆桌旁,每人面前有一只碗,碗里有面条,每两人之间放一只筷子;
- (2)每个哲学家的行为是思考,感到饥饿,然后吃饭;
- (3)为了吃饭,每个哲学家必须拿到两只筷子并且每个人只能直接从自己的左边或右边去取筷子。
算法描述
为每个筷子设置一个互斥型信号量semaphore chopstick[5]={1,1,1,1,1},一个哲学家通过在相应信号量上执行P操作拿起一支筷子,通过V操作放下一支筷子
平常算法如下
do{
...
思考;
...
P(chopstick[i]); //拿起左边筷子
P(chopstick[(i + 1) % 5]); //拿起右边筷子
...
用餐;
...
V(chopstick[i]); //放下左边筷子
V(chopstick[(i + 1) % 5]); //放下右边筷子
...
} while(true);
存在问题
虽然可以保证互斥使用筷子,但有可能产生死锁。假设5个哲学家同时拿起各自左边的筷子,于是5个信号量都为0。此时,当每个哲学家企图拿起他右边的筷子时,会出现循环等待现象--死锁
改进
采用资源有序分配算法(也就是破坏死锁的四个必要条件之一循环等待条件,查看进程二文章),给每个筷子编号,规定每个哲学家先拿编号小的筷子再拿编号大的筷子。哲学家i (1≤i≤4)不变。最后一个哲学家承接收尾,所以不能先拿左边,再拿右边
第五个哲学家的程序改进如下:
do{
...
思考;
...
P(chopstick[1]); //拿起右边筷子
P(chopstick[5]); //拿左边筷子
...
用餐;
...
V(chopstick[i]); //放下左边筷子
V(chopstick[(i + 1) % 5]); //放下左边筷子
...
} while(true);
改进思路
当每个哲学家都想就餐时,可能有4个哲学家都已拿到自己左边的筷子,而剩下的第5个哲学家拿不到编号小的筷子而等待,该哲学家不可能去拿另一支筷子。因此,四个哲学家中的一个哲学家就有机会拿起其右边的筷子而可以用餐,就餐后放下一双筷子,以使另一个哲学家又可以得到右边的筷子去用餐,同样的,其他的哲学家也都可以先后吃饭,从而防止死锁
