04月
08

发表于 • 字数统计 6750 • 被 998 人看爆

定义

是一种平衡的多路查找树

—棵m(m≥3)阶的B树，或为空树，或为满足下列性质的m叉树:

  • ①每个结点至少包含下列信息域:
    (n，p0，k1，p1，k2，...，kn,pn)
    其中，n为关键字的个数;
    ki(1 ≤ i ≤ n)为关键字，且ki< ki+1（1≤i< n-1);
    pi(0 ≤ i < n)为指向子树根结点的指针，且pi所指向子树中所有结点的关键字均小于ki+1， pn所指子树中所有结点关键字均大于kn
  • ②树中每个结点至多有m棵子树。
  • ③若树为非空，则根结点至少有1个关键字，至多有m-1个关键字。因此，若根结点不是叶子，则它至少有两棵子树。
  • ④所有的叶结点都在同一层上，并且不带信息（可以看作是外部结点或查找失败的结点，实际上这些结点不存在，指向它们的指针均为空)，叶子的层数为树的高度h。
  • ⑤每个非根结点中所包含的关键字个数满足:[m/2]-1≤n≤m-1。因为每个内部结点的度数正好是关键字总数加1，所以，除根结点之外的所有非终端结点（非叶子结点的最下层的结点称为终端结点）至少有[m/2]棵子树，至多有m棵子树。

实例

下图是一棵4阶的B树
B树实例.png

一颗4阶的B树，其深度为3
同一二叉排序树一样，关键字插入的次序不同，将可能生成不同结构的B树
该树共三层，所有叶子结点均在第三层上
在一颗4阶的B树中，每个结点的关键字个数最少为[m / 2] - 1 = [4 / 2] - 1 = 1，最多为m - 1 = 4 - 1 = 3
每个结点的子树数目最少为[m / 2] = [4 / 2] = 2，最多为m = 4

B树的结点类型定义

#define m 10        //m为B树的阶，结点中关键字最多可有m-1个
typedef struct node
{
    int keynum;         //结点中关键字个数，即结点的大小
    KeyType key[m];     //关键字向量，key[0]不用
    struct *parent;     //指向双亲结点
    struct node *ptr[m];    //子树指针向量
}BTNode;

typedef BTNode *BTree;

B树上的插入

在B树中插入一个结点的过程：先在最低层的某个非终端结点中添加一个关键字。若该结点中关键字的个数不超过m-1，则插入完成，否则要产生结点"分裂"。"分裂"结点时把结点分成两个，将中间的一个关键字拿出来插入到该结点的双亲结点上，如果双亲结点中已有m-1个关键字，则插入后将引起双亲结点的分裂，这一过程可能波及B树的根结点，引起根结点的分裂，从而使B树长高一层。

例1

试画出将关键字序列:24，45，53，90，3，50，30，61，12，70，100依次插入一棵初始为空的4阶B树中的过程。

解答

B树插入示例.png
过程：
因为要求生成的是4阶B树，即m = 4，也就是每个结点最大容纳3个关键字，超过就要进行分裂
 1.当三个关键字24，45，53插入到一个新结点(空白结点)，它既是根结点也是叶结点。如上图(0)插入
 2.当插入第四个关键字90时，[24 45 53 90]，关键字数等于4，违反B树的性质，因此根据B树插入算法，要进行分裂，将该结点以关键字key[m / 2] = key[2]为划分点，45为第二个关键字，将其拿出，并将45插入到当前结点的双亲结点上，作为根结点，其它分裂成[24] [53 90]。如上图(a)
 3.当插入关键字3时，3比45小，插入到它的左结点上，45的左结点未超过3个数(B树性质，4阶B树，每个结点最多容纳3个关键字(m-1)),可以放进去，如上图(b)
 4.插入关键字50，比根结点(45)大，要放到它的右结点上，右结点关键字数未超出，可以放进去。如上图(c)
 5.插入关键字30，比根结点(45)小，要放到左结点上，并且左结点关键字树未超出，可以放进去。如上图(d)
 6.插入关键字61，比根结点(45)大，要放到右结点上，右结点[50 53 61 90]关键字数超出，此时就要分裂，将该结点第二个关键53(由(m / 2)得)拿到根结点上，其它分裂成[50] [61 90]。如上图(e)
 7.插入关键12，12比根结点小，插入到左结点，此时左结点[3 12 24 30]超出，进行分裂，将第二个关键字12拿到根结点上，分裂成[3] [24 30]。如上图(f)
 8.插入关键字70，70比根结点都大，插入到最右结点上，[61 70 90]。如上图(g)
 9.插入关键字100，比根结点都大，插入到最右边结点，右结点[61 70 90 100]超出分裂，分裂成[61] [90 100]，并拿出第二个关键字70，放到根结点上[12 45 53 70]，根结点也超出，分裂[12] [53 70]，拿出第二个关键字45，将其放到根结点上。如上图(h)

例2

已知3阶B树如图所示
B树插入例题.png

(1)画出将关键字6插入之后的B树;
(2)画出在(1)所得树中插入关键字2之后的B树。

B树插入例题解答.png

B树上的删除

(1)删除后不小[m/2]

 若需删除关键字所在结点中的关键字数目不小于[m/2]，则只需要该结点中关键字和相应的指针删除。

示例

画出删除图(a)中所示3阶B树上的关键字3后的B树。

B树删除1示例.png

解析

【解析】在3阶B树中，要册除的关键字所在的结点有2个关键字，直接删除该关键字和相应的指针即可。
【答案】册除关键字3后的B权树如图(b)所示

(2)删除后等于[m/2]-1

 若需删除关键字所在结点中的关键字数目等于[m/2]-1，即关键字数目已是最小值，直接删除该关键字会破坏B树的性质。册除这样关键字分两种情况处理:

  • ①若所删结点的左(或右)邻兄弟结点中的关键字数目不小于[m/2]，则将其兄弟结点中的最大(或最小)的关键字上移至双亲结点中，而将双亲结点中相应的关键字移至删除关键字所在结点中。

示例1

画出删除上面(b）图中的关键字12后的B树。
B树删除2示例1.png

要删除关键字12，则需要将其右邻兄弟结点中30上移到其双亲结点中。而将双亲结点中的24移到被删结点中

  • ②若需删除关键字所在结点及其相邻的左、右兄弟(或只有一个兄弟)结点中关键字数目均等于[m/2]-1，则按上述情况①的移动操作就不能实现。此时，就需要将被删结点与其左兄弟或右兄弟结点进行"合并"。假设该结点有右邻兄弟(对左邻兄弟类似)，其兄弟结点地址由双亲结点中指针pi指定，在删除关键字之后，它所在结点中剩余的指针加上双亲结点中的关键字ki一起，合并到pi指定的兄弟结点中

示例2

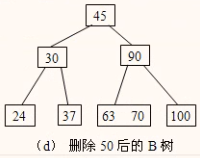
画出册除上面(c)图中的关键字50后的B树。

解析

【解析】删除50，需要将63和70合并，90单独作为双亲结点。
【答案】删除(c)图中的关键字50后的B树如图(d)所示。
B树删除2示例2.png

上述情况②如果因"合并"操作引起对父结点中关键字的删除，又可能要合并结点，这一过程可能彼及根，引起对根结点中关键字的删除，从而可能使B树的高度降低一层。

示例3

画出删除上面(d)图中的关键字24后的B树。

解答

【解析】删除24后，30需要37进行合并，这样需要45和90合并才能满足B树的性质，使B树的高度降低一层。
【答案】册除(d)图中的关键字24后的B树如图(e)所示。
B树删除2示例3.png

B树上的查找

在B树上进行查找过程与二叉排序树类似，都是经过一条从树根结点到待查关键字所在结点的查找路径，不过对路径中每个结点的比较过程比在二叉排序树的情况下复杂一些。因此，又称B树为多路查找树
主要操作：在B树中查找结点、在结点中查找关键字

二叉排序树知识

查找算法思想

在B树中查找一个关键字等于给定值K的具体过程：若B树为非空，则首先取出树根结点，将给定值K依次与关键字向量中从高下标端(key[keymum])开始的每个关键字进行比较，直到K≥Ki (0≤i≤n=keynum，用key[0]作为中止标志，存放给定的查找值)为止，此时，若K=Ki且i>0，则表明查找成功，返回具有该关键字的结点的存储位置及K在key[1...keynum]中的位置；否则,其值为K的关键字只可能落在当前结点的pi所指向的子树上，接着只要在该子树上继续进行查找即可。这样，每取出一个结点比较后就下移一层，直到查找成功，或被查找的子树为空(即查找失败)为止

算法描述

假定指向B树根结点的指针用T表示，待查找的关键字用K表示

BTNode * SearchBTree (BTree T,KeyType K,int* pos) 
{
    //从树根指针为T的B树上查找关键字为K的对应结点的存储地址及K在其中的
    //位置*pos，查找失败返回NULL，*pos无定义
    int i;
    BTNode *p=T;
    while (p!=NULL)      //从根结点开始起依次向下一层查找
    {
        i=p->keynum;    //把结点中关键字个数赋给i
        p->key[0]=K;    //设置哨兵，顺序查找key[0...keynum]
        while(K<p-> key[i])     //从后向前查找第1个小于等于K的关键字
            i--;
        
        if(K==key[i] && i>0)
        {
            *pos=i; 
            return p;
            
        }
        else
            p=p->ptr[i];
    }
    
    return NULL;
    
}

算法分析

分析下图所示B树，查找18的过程
B树查找实例分析.png

解析

k0为哨兵，相当于冒泡排序的副本temp
先和根结点a比较。把K=18赋给K0。因为该结点的keynum=1，所以K与a中k1比较，K=18小于k1的值48，再同a结点中k0比较，
此时k0=K，因为i=0，所以接着取出a结点的p0指向的结点b，用K与b结点中的k2=32进行比较，k=18< k2=32,而K=18>k1=16，
所以再取出b结点的p1所指向的结点e，因为K=k1，因此查找成功，返回e结点的存储地址以及k1的位置pos=1。

B+树

B+树是一种常用于文件组织的B树的变形树。

一棵m阶的B+树和m阶的B树的差异在于:

  • (1)有k个孩子的结点必含有k个关键字。
  • (2)所有的叶结点中包含了关键字的信息及指向相应结点的指针，且叶子结点本身依照关键字的大小从小到大顺序链接。
  • (3)所有非终端结点可看成是索引部分，结点中仅含有其子树(根结点)中的最大关键字(或最小)关键字。

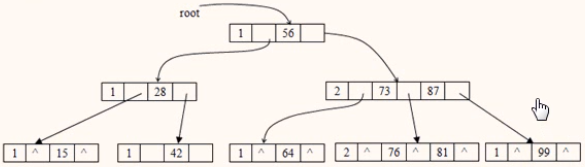
例

下图所示是一棵3阶的B+树。通常在B+树上有两个头指针root和sqt，前者指向根结点，后者指向关键字最小的叶子结点。
因此，可以对B+树进行两种查找运算:

  • (1)一种是从最小关键字起进行顺序查找
  • (2)另一种是从根结点开始进行随机查找。

B树查找示例.png

在B+树上进行随机查找、插入和删除的过程，基本上与B树类似。只是在查找时，若非叶结点上的关键字等于给定值，并不终止，而是继续向下直到叶子结点。因此，在B+树中，不管查找成功与否，每次查找都是走了一条从根到叶子结点的路径。B+树上查找的分析类似于B树；B+树的插入仅在叶子结点进行，当结点中的关键字个数大于m时要分裂成两个结点，它们所含关键字的个数分别为[(m+1/2]和(m+1)/2]，并且它们的双亲结点中应同时包含这两个结点中的最大关键字。B+树的删除也仅在叶子结点进行，当叶子结点中的最大关键字被删除时，其在非终端结点中的值可以作为一个“分界关键字”存在。若因删除而使结点中关键字的个数少于[m/27时，则可能要和该节点的兄弟结点合并，其合并过程也与B树也类似

分享到：