定义
是限定在表的一端进行插入和珊除运算的线性表,通常将插入、删除的一端称为栈项(top),另一端称为栈底(bottom)。不含元素的空表称为空栈。
栈的修改是按后进先出的原则进行的,因此,栈又称为后进先出(Last In First Out)的线性表,简称为LIFO表。
例题
如图所示,设输入元素的顺序是(A,B,C,D),通过栈的变换,在输出端可得到各种排列。若输出序列的第一个元素为D,则输出序列_____
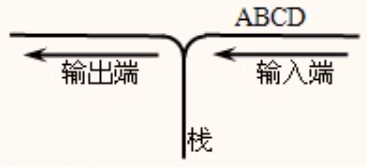
解析
【答案】DCBA
【解析】根据堆栈'先进后出"的原则,若输出序列的第一个元素为D,则JABCD入栈,输出序列为DCBA
栈的基本运算
- (1)置空栈InitStack(&S):构造一个空栈S。
- (2)判栈空StackEmpty(S):若栈s为空栈,则返回TRIE,否则返回FALSE。
- (3)判栈满StackFull(S):若栈s为满栈,则返回TRuE,否则返回FALSE。
- (4)进栈(又称入核或插入):Push(&S,x):将元素x插入S栈的栈顶。
- (5)退栈(又称出栈或删除)Pop(&s):若栈s为非空,则将s的栈顶元素删除,并返回栈顶元素。
- (6)取栈顶元素GetTop(S):若s栈为非空,则返回栈顶元素,但不改变栈的状态。
栈的顺序存储结构
顺序栈的概念
栈的顺序存储结构称为顺序栈。顺序栈也是用数组实现的,栈底位置是固定不变的,将栈底位置设置在数组的最低端〈(即下标为0)﹔栈顶位置是随着进栈和退栈操作而变化的,一个整型量top来指示当前栈顶位置,通常称top为栈顶指针。
顺序栈的类型描述
#define stackSize 100 //栈空间的大小应根据实际需要来定义,这里假设为100
typedef char DataType; //DataType的类型可根据实际情况而定,这里假设为char
typedef Struct
{
DataType data[stackSize]; //数组data用来存放表结点
int top; //表示栈顶指针
}SeqStack; //栈的数据类型
seqStack s; //s为栈类型的变量
栈的顺序实现
(1)置空栈
void InitStack(SeqStack *S)
{
//置空顺序栈。由于c语言数组下标是从0开始,所以栈中元素亦从0开始
//存储,因此空栈时栈顶指针不能是0,而只能是-1
S->top=-1;
}
(2)判栈空
int StackEmpty(SeqStack *S)
{
return S->top==-1; //如果栈空则S->top==-1的值为1,返回1,反之,返回0
}
(3)判栈满
int StackFull(SeqStack *S)
{
return S->top==StackSize-1; //如果栈满则s->top== StackSize -1的值为1,返回1,反之,返回0
}
(4)进栈(入栈)
void Push(SeqStack *S,DataType x)
{
if(StackFull(S)) //调用判满函数
{
printf("stack overflow");
}
else
{
S->top=S->top+1; //栈顶指针加1
s->data[S->top]=x; //将x入栈
}
}
(5)退栈(出栈)
DataType Pop(SeqStack *S)
{
if(StackEpty(S)) //调用判空函数
{
printf("Stack underflow");
exit(O); //出错退出处理
}
else {
return s->data[S->top--]; //返回栈顶元素,栈顶指针减1
}
}
(6)取栈源元素(不改变栈顶指针)
DataType GetTop(SeqStack *S)
{
if(StackEmpty(S)) //调用判空函数
{
printf("stack empty");
exit(0); //出错退出处理
}
else
{
return S->data[s->top]; //返回栈顶元素,注意:栈顶指针不动
}
}
另外,同时使用多个栈时,多个栈分配在同一个顺序存储空间内,即让多个栈共享存储空间,则可以相互进行调节,既节约了空间,又可降低发生溢出的频率。当程序中同时使用两个栈时,可以将两个栈的栈底分别设在顺序存储空间的两端,让两个栈顶各自向中间延伸。
栈的链式存储结构
(1)链栈的概念
栈的链式存储结构称为链栈。它是运算受限的单链表,其插入和删除操作仅限制在表头位置上(栈顶)进行,因此不必设置头结点,将单链表的头指针head改为栈顶指针top即可。
(2)栈的类型定义
typedef struct stacknode
{
DataType data;
struct stacknode *next;
}StackNode; //定义结点
typedef StackNode *Linkstack;
LinkStack top; //定义栈顶指针top
链栈的基本运算
(1)判栈空
int StackEmpty(LinkStack top)
{
return top==NULL; //栈空top==NULL的值为1,返回1,否则返回0
}
(2)进栈(入栈)
LinkStack Push(LinkStack top,DataType x) //将x插入栈顶
{ //无需判满
StackNode *P;
p=(StackNode *)malloc(Sizeof(StackNode)); //申请新的结点
p->data=x; //申请新的结点
p->next=top; //新结点*p插入栈顶
top=p; //更新栈顶指针top
return top;
}
(3)退栈(出栈)
LinkStack Pop(LinkStack top,DataType *x)
{
StackNode*p=top; //保存栈顶指针
if(StackEpty(top)) //栈为空
{
printf("stack empty"); //出错退出处理
exit(0);
}
else {
*x=p->data; //保存删除结点值,并带回
top=p->next; //栈顶指针指向下一个结点
free(p); //删除P指向的结点
return top; //并返删除后的栈顶指针
}
}
(4)取栈顶元素
DataType GetTop (LinkStack top)
{
if(StackEpty(top)) //栈为空
{
printf("stack empty");
exit(0); //出错退出处理
}
e1se {
return top->data; //返回栈项结点值
}
}
例题1
己知链栈的结点结构为[data][next],栈顶指针为top,则实现将指针p所指结点插入栈顶的语句依次为____和____
解析
【答案】p->next=top; top=p;
【解析】根据栈的进栈操作的规则,将指针p所指结点插入栈顶的语句依次为p->next=top; top=p。
例题2
对于输入的一个算术表达式字符串,试写一算法判断其中圆括号是否匹配若匹配则返回TRUE,否则返回FALSE。
分析
利用栈的操作来实现:循环读入表达式中的字符,如遇左括号"("就进栈,遇右括号")"则判断栈是否为空,若为空,则返回FALSB,否则退栈,循环结束后再判断栈是否为空,若栈空则说明括号匹配,否则说明不匹配。
算法描述
int Expr()
{
SeqStack S;
DataType ch,x;
InitStack(&S); //初始化栈S
ch=getchar ();
while(ch!='\n')
{
if(ch=='(')
{
Push(&s,ch); //遇左括号进栈
}
else
{
if(ch==')')
{
if(StackEpty(&s)) //遇右括号如果栈空,说明不匹配,返回0
return 0;
else
x=Pop(&s); //遇右括号退栈
}
}
ch=getchar(); //读入下一个字符
}
if(StackEmpty(&S))
return 1; //最后栈空,说明匹配,返回1
else
return 0;
}
例题3
利用顺序栈的基本运算,试设计一个算法,判断一个输入字符串是否具有中心对称(也就是所谓的"回文",即正读和反读均相同的字符序列),例如adbaba和abcba都是中心对称的字符串。
分析
从中间向两头进行比较,若完全相同,则该字符串是中心对称,否则不是。这就要首先求出字符串串的长度,然后将前一半字符入栈,再利用退栈操作将其与后一半字符进行比较。
算法描述
int synmetry(char str[])
{
SeqStack S;
int j,k,i=0;
InitStack(&S);
while(Str[i]!='\0') i++; //求串长度
for(j=0; j<i/2; j++)
{
Push(&s,str[j]); //前一半字符入栈
}
k=(i+1)/2; //后一半字符在串中的起始位置
//特别注意这条命令怎么处理奇偶数个字符的。
for(j=k; j<i; j++) //后一半字符与栈中字符比较
{
if(str[j]!=Pop(&s))
{
return 0; //有不相同字符,即不对称
}
}
return 1; //完全相同,即对称
}
例题4
设一个栈的输入序列为:1,2,3,4,5,则下列序列中不可能是栈的输出序列的是()
A. 1,2,3,4,5 B. 5,4,3,2,l
C. 2,3,4,5,1 D. 4,1,2,3,5
解析
【答案】D
【分析】根据堆栈"先进后出""的原则和经验,很容易判断选项A和B可以是栈的输出序列;1,2进栈,2出栈,3进3出,4进4出,5进5出,最后1出栈就可以得到选项c的序列。选项D:要想4第一个输出,必须1、2、3、4进栈,然后4出栈,接下来1不可能先与3和2出栈,所以不可能是栈的输出序列。
