最短路径
最短路径问题的提法很多,在这里仅讨论单源最短路径问题:从某个源点S∈ V到G中其余各顶点的最短路径。
对于求多源点的最短路径问题,可以用每个顶点作为源点调用一次单源最短路径问题算法予以解决。
例
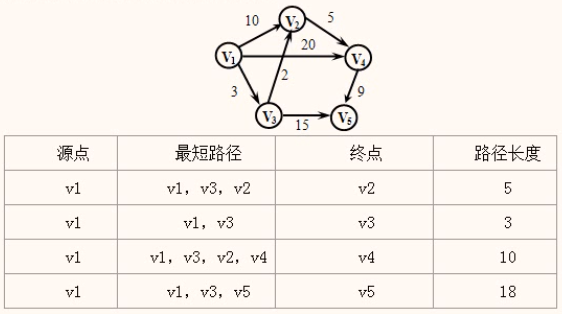
下图所示带权有向图,假定以v1为源点,则v1到其他各顶点的最短路径下表所示。
分析
从图可看出,顶点v1到v4的路径有3条(v1, v2, v4),(v1, v4),(v1, v3, v2, v4),其路径长度分别为15,20和10,因此,v1到v4的最短路径为(v1, v3, v2, v4)
迪杰斯特拉(Dijkstra)算法
该算法是典型的最短路径路由算法,用于计算一个顶点到其他所有顶点的最短路径。
主要特点是以起始点为中心向外层扩展,直到扩展到终点为止。
按路径长度递增的顺序产生诸顶点的最短路径算法
算法思想
设有向图G=<V, E>,其中,V={1, 2,...,n},cost是表示G的邻接矩阵,cost[i][j]表示有向边<i, j>的权。若不存在有向边<i, j>,则cost[i][j]的权无穷大(假定取值为32 757)。设S是一个集合,其中每个元素表示一个顶点,从源点到这些顶点的最短举例已经求出。设v1为源点,集合S的初态只包含顶点v1。数组dist记录从源点到其它各顶点当前的最短距离,其初值为dist[i]=cost[v1][i],i=2,...,n。从S之外的顶点集合V-S中选出一个顶点w,使dist[w]的值最小。从源点到达w只通过S中的顶点,把w加入集合S中并调整dist中记录的从源点到V-S中每个顶点v的距离,即从原来的dist[v]和dist[w]+cost[w][v]中选择较小的值作为新的dist[v]。重复上述过程,直到S中包含V中其余顶点的最短路径
简述: 创建三个数组,数组S记录了当前从源点到该顶点存在最短路径的顶点集合﹔数组dist(简称D)记录当前状态源点到图中其余各顶点之间的最短路径长度;数组path(简称P)是最短路径的路径数组,其中path[j]表示从源点到顶点j的最短路径上顶点的前驱顶点。每一次循环都是从数组D中选择未被加入到数组S中的顶点到源点路径最短的顶点加入到数组S中,然后对数组D和数组P进行修改,直到所有顶点都加到了数组s中为止。
算法结果: S记录了从源点到该顶点存在最短路径的顶点集合,数组dist记录了从源点到V中其余各顶点之间的最短路径长度,path是最短路径的路径数组,其中path[i]表示从源点到顶点i的最短路径上顶点的前驱顶点
算法描述
typedef int Distance[n+1];
typedef int Path[n+1];
void Dijkstra(MGraph G, int v1, int n) {
//用Dijkstra算法求有向图G的v1顶点到其他顶点v的最短路径P[v]及其权D[v]
//设G是有向网的邻接矩阵,若边<i, j>不存在,则G[i][j] = Maxint
//S[v]为真当且仅当v∈s,即已求得从v1到v的最短路径
int D2[MVNum], P2[MVNum];
int v, i, w, min;
boolean S[MVNum];
for(v=1; v<=n; v++) { //初始化S和D
S[v] = false; //置空最短路径终点集
D2[V] = G.arcs[v1][v]; //置初始的最短路径值
if(D2[v] < Maxint)
P2[v] = v1; //v1是v的前趋(双亲)
else
P2[v]=0; //v无前趋
}
D2[v1] = 0;
S[v1] = true; //S集初始时只有源点,源点到源点的距离为0
//开始循环,每次求得v1到某个v顶点的最短路径,并加v到s集中
for(i=2; i<n; i++) { //其余n-1个顶点
min = Maxint;
for(w=1; w<=n; w++) {
if(!S[w] && D2[w]<min) { //w顶点距离v1顶点更近
V=w;
min = D2[w];
}
S[v] = true;
for(w = 1; w <= n; w++) { //更新当前最短路径及距离
if(!S[w] && (D2[v] + G.arcs[v][w] < D2[w]>)) { //修改D2[w]和P2[w],w∈V-S
D2[w] = D2[v] + G.arcs[v][w];
P2[w] = v;
}
}
}
}
}
例1
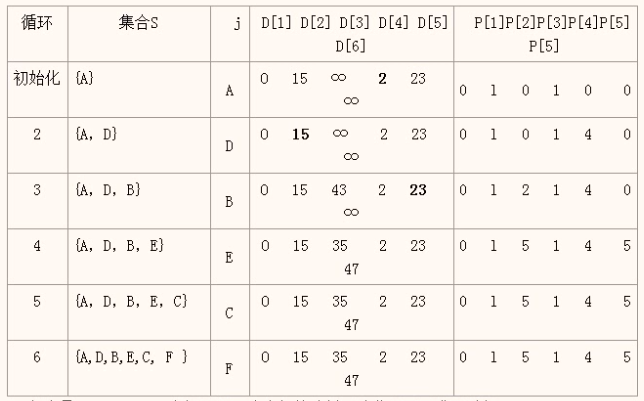
下图有向图G10和其带权邻接矩阵,若对其执行迪杰斯特拉算法,给出求解过程

解答
对G10执行迪杰斯特拉算法,则从v1到其余各顶点的最短路径以及运算过程中D数组的变化状态如下
例2
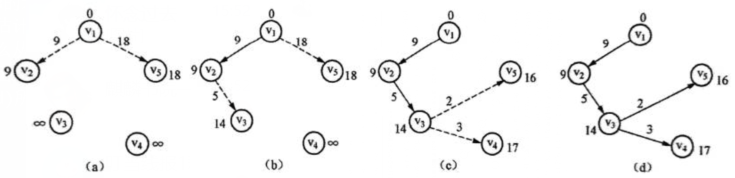
已知有向图如图所示,根据迪杰斯特拉算法画出求源点v1开始的单源最短路径的过程示意图,以及算法的动态执行过程。

分析
按迪杰斯特拉算法及题目的要求,初始时记录从源点到该顶点存在最短路径的顶点集合S中只有一个源点v1,初始N=V-S顶点集中vj(j=2,3,4,5)的估计距离D[j]均为有向边<v1, vj>上的权值。因为边<v1,v,3>和边<v1,v4>不存在,所以 D[3]=D[4]=∞,如图(a)所示。在图(a)中,当前N集中顶点v2的估计距离D[2]=9最小,故将其加入到S集中,即从源点v1到顶点v2的最短路径已找到,其长度为9。因为顶点v2到顶点v3有一条权为5的边,所以从源点v1到v3且中间经过顶点v2的新路经<1,2,3>的长度是14,它小于顶点v3的原估计距离∞,因此必须将顶点v3的估计距离D[3]调整为14。顶点v4、v5的原估计距离没有因为新顶点v3的产生而减小,故无需调整,如图(b)所示。在当前N顶点集中顶点v3的估计距离D[3]=14最小,故将其加入到集合S中;又因为新加入S的顶点v3到顶点v4有一条权为3的边,所以从源点v1到顶点v4中间经过的新路径<1,2,3,4>的长度是17,它小于顶点v4的原估计值∞,因此必须将顶点v4的估计距离 D[4]调整为17。而顶点v3到顶点v5有一条权为2的边,那么从源点v1到顶点v5中间经过的新路径<1,2,3,5>的长度是16,它小于顶点v5的原估计值18,因此将顶点ve5的估计距离D[5]调整为16,如图(c)所示。最后将顶点v5、v4加入到集S中,如图(d)所示。
例3
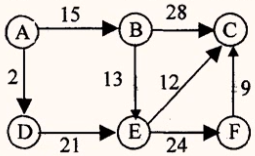
已知有向图如下图所示,其中顶点A到顶点C的最短路径长度是____
解答
【答案】35
【解析】迪杰斯特拉算法的动态执行情况
可见顶点A到顶点C的最短路径为<A、D、E、C>长度是2+21+12=35。
拓扑排序
对一有向图,如果从Vi到Vj存在一条路径,且在由图中所有顶点构成的线性序列中,Vi总在Vj之前,那么这样的线性序列就被称为拓扑序列。
构造一个有向图的拓扑序列的过程称为拓扑排序。
一个有向图必须满足两个条件才存在拓扑序列:
- ①初始时有向图中必须至少有一个入度为0的顶点。
- ②有向图中不存在回路。
满足以上两条的有向图称为AOV网
AOV网
也称有无环图(DAG)称为顶点活动网,简称AOV网
AOV网中不存在有向环(即回路)
在AOV网中,若从顶点vi到顶点vj有一条有向路径,则顶点vi是vj的前趋,vj是vi的后继。
若<vi, vj>是网中一条弧,则顶点vi是vj的直接前趋,vj是vi的直接后继
例
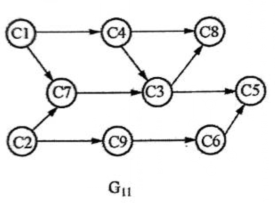
例如,一个计算机应用专业的学生必须修完一系列基本课程(如下表所示),其中有些课程是基础课,它们独立于其他课程,如“高等数学”,它无需先选修其他课程;而在学习“数据结构”之前,就必须先选修完课程“离散数学”和“算法语言”。若用AOV网来表示这种课程安排的先后关系,如下图中图G11所示。图中每个顶点代表一门课程,每条有向边代表起点课程是终点课程的先修课程,从图中可以清楚地看出各课程之间的先修和后修的关系。例如,课程C4的先修课程为C1,后续课程为C3和C8;C5的先修课程为C3和C6,而它无后续课程。
| 课程编号 | 课程名称 | 先修课程 |
|---|---|---|
| C1 | 计算机基础 | 无 |
| C2 | 高等数学 | 无 |
| C3 | 数据结构 | C4、C7 |
| C4 | 算法语言 | C1 |
| C5 | 操作系统 | C3、C6 |
| C6 | 计算机原理 | C9 |
| C7 | 离散数学 | C1、C2 |
| C8 | 编译技术 | C3、C4 |
| C9 | 普通物理 | C2 |
拓扑排序
由AOV网构造拓扑序列的过程称为拓扑排序
拓扑排序过程
- ①从有向图中选择一个入度为0的顶点;
- ②从有向图中将该顶点以及由该顶点发出的所有弧全部删除;
- ③重复上述过程,直到剩余的网中不再存在入度为0的顶点。
算法描述
分析
在拓扑排序算法中,需要设置一个含n个元素的一维数组,假定用inde表示,用它来保存AOV 网中每个顶点的入度值。设一个栈暂存所有入度为零的顶点,以后每次选入度为零的顶点时,只需要做出栈操作即可。算法中删除顶点及其所有边的操作只需要检查出栈的顶点vi的出边表,把每条出边<vi, vj>的终点vj所对应的入度inde[j]减1,若vj的入度为零,则将j入栈。
算法描述
#define N 20
void TopuSort(ALGraph G. int n) {
//对用邻接表G表示的有向图进行拓扑排序
int i, j, m=0; //m用来统计输出的顶点数
int inde[N]; //定义入度数组
Seqstack S;
EdgeNode *p;
for(i=0; i<n; i++) //初始化数组inde的每个元素值为0
{
inde[i]=0;
}
for(i=0; i<n; i++){ //扫描每个顶点vi的出边表,统计每个顶点的入度数
p=G[i].link;
while(p) {
inde[p->adjvex]++;
p=p->next;
}
}
InitStack(&S); //初始化栈,并将入度为零的顶点i入栈
for(i=0; i<n; i++) {
if(inde[i] == 0)
Push(&s,i);
}
while(!stackEmpty(&S)) { //拓扑排序开始
i=Pop(&S); //删除入度为0的顶点
printf("v%d ",i); //输出一个顶点
m++;
p=G[i].link;
while(p) { //扫描顶点i的出边表
j = p->adjvex;
inde[j]--; //vj的入度减1,相当于删除边<vi, vj>
if(inde[j] == 0) //若vj的入度为0,则入栈
Push(&S, j);
p = p->next;
}
}
if(m < n) //当输出的顶点数小于图中的顶点数时,说明图有回路,排序失败
printf("The Graph has a cycle!");
}
拓扑排序算法的时间复杂度为O(n+e) 。
例1
对下图进行拓扑排序

过程
按照拓扑排序步骤,选择入度为0的顶点(C1或C2),将其删除。然后再查找入度为0的顶点(C4、C7、C9),将其删除,重复其上步骤,直到没有入度为0的顶点
可得到两个拓扑排序,还有很多就不列举了
C1、C4、C2、C7、C3、C8、C9、C6、C5
C2、C9、C6、C1、C7、C4、C3、C5、C8
例2
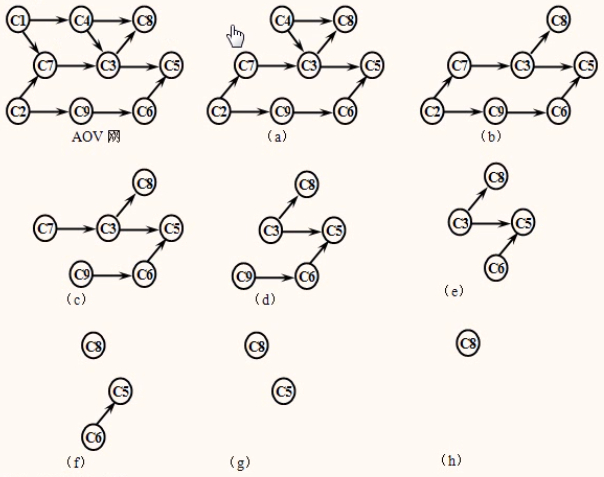
过程
上图中顶点C1和C2的入度均为零,可以输出任何一个。若先输出C1,则在删除相应的边后便得到(a),该图中C4、C2的入度数为零,输出C4,则得图(b),依此类推,直到得到图(h),这时仅有一个入度为零的顶点C8,输出C8后整个拓扑排序过程结束。
以C1作为第一个输出,可得拓扑排序序列为C1、C4、C2、C7、C9、C3、C6、C5、C8,
以C2作为第一个输出,可得拓扑排序序列为C2、C1、C9、C7、C4、C3、C6、C8、C5.