定义
"散列(Hash)":既是一种线性表存储方式,又是一种查找方法。这种查找方法称为散列查找。
通过对记录的关键字值进行某种运算直接求出记录的地址,是一种由关键字到地址的直接转换方法,不需要反复比较
基本思想
通过由散列函数决定的键值与散列地址之间的对应关系来实现存储组织和查找运算。
具体:
以线性表中的每个元素的关键字key为自变量,通过一种函数H(key)计算出函数值,把这个函数值解释为一块连续存储空间得到单元地址(即下标),将该元素存储到这个单元中。
散列存储中使用的函数H(key)成为散列函数或哈希函数,它实现关键字到存储地址的映射(或称转换)
H(key)的值称为散列地址或哈希地址,使用的数组空间是线性表进行散列存储的地址空间,所以被称为散列表或哈希表
当在散列表上进行查找时,首先根据给定的关键字key,用散列存储时使用的同一散列函数H(key)计算出散列地址,然后按此地址从散列表中取得对应的元素
实例分析
有个线性表A=(31,62,74,36,49,77),其中每个整数可以是元素本身,也可以仅是元素的关键字,假设散列函数为:H(key)=key%m,即用元素的关键字key整除m,取其余数作为存储该元素的散列地址,m一般取小于或等于散列表长的最大素数,在这里取m=11,表长也为11,因此可得到每个元素的的散列地址:
H(31)=31%11=9; H(62)=62%11=7;H(74)=74%11=8;
H(36)=36%11=3; H(49)=49%11=5;H(77)=77%11=0;
将其放置到散列表中,则存储结构为:

问题
若在上面散列表中插入元素88、7等会出现冲突。
H(88) = 88%11 = 8; H(7) = 7%11 = 0
采用散列技术时需要考虑的两个主要问题是:①如何构造(选择)"均匀的"散列函数?②用什么方法解决冲突?
散列函数的构造方法
目标:使散列地址仅可能均匀地分布在散列空间上,同时使计算简单
1.直接地址法
直接地址法是以关键字key本身或关键字加上某个常量C作为散列地址的方法。
对应的散列函数H(key)为:H(key)=key+C
特点:
方法计算简单,并且没有冲突。
它适合于关键字的分布基本连续的情况,若关键字分布不连续,空号较多,将会造成较大的空间浪费。
2.数字分析法
数字分析法是假设有一组关键字,每个关键字由n位数字组成,数字分析法是从中提取数字分布比较均匀的若干位作为散列地址。
例
有一组6位数字组成的关键字,如下表所示
| 关键字 | 散列地址(0...99) |
|---|---|
| 912356 | 13 |
| 952456 | 54 |
| 964852 | 68 |
| 982166 | 81 |
| 892556 | 95 |
| ... | ... |
| 872265 | 72 |
分析这组关键字发现,第1、3、5和6位(个位、百位)数组分布不均匀,如第1位数字全是9,或者8,第3位基本上都是2,第5、6两位也都基本上是5和6,故这4位不可取,而第2、4两位数字分布比较均匀,因此可取关键字中第2、4位的组合作为散列地址
3.除余数法
除余数法是一种最简单也最常用的一种散列函数构造方法。
散列函数:H(k)=k%p
其中,p最好选取小于或等于表长m的最大素数。如表长为20,那么p选19,若表长为25,则p可选23....
表长m与模p的关系可按下表对应:
m = 8、16、32、64、128、256、512、1024....
p = 7、13、31、61、127、251、503、1019....
上面的实例分析已经讲过
4.平方取中法
平方取中法是取关键字平方的中间几位作为散列地址的方法
例
一组关键字组合(0100,0110,0111,1001,1010,1110)
平方后得到数据集合(0010000,0012100,0012321,1002001,1020100,123210)
那么若表长为1000,则可取其中第3、4和5位作为对应的散列地址(100,121,123,020,201,321)
5.叠加法
折叠法是首先把关键字分割成位数相同的几段(最后一段的位数可少一些),段的位数取决于散列地址的位数,由实际情况而定,然后将它们的叠加和(舍去最高进位)作为散列地址的方法
折叠法又分为移位叠加和边界叠加。
移位叠加是将各段的最低对齐,然后相加
边界叠加则是将两个相邻的段沿边界来回折叠,然后对齐相加
例
关键字k=98 123 658,散列地址为3位,则将关键字从左到右每三位一段进行划分,得到的三个段为981、236和58,叠加后值为1275,取低3位275作为关键字98 123 658的元素的散列地址
解决冲突的方法
1.开放定址法
开放定址法的思想:使用某种方法在散列表中形成一个探查序列,沿着此序列逐个单元进行查找,直到找到一个空闲的单元时将新结点存入其中。
开放定址法又分为线性探插法、二次探查法和双重散列法。
例
假设散列表空间位T[0...m-1],散列函数为H(key),则开放定址法的一般形式为:
hi = (H(key) + di) % m 0≤i≤m-1
其中di为增量序列,m为散列表长。h0 = H(key)为初始探查地址(假设d0 = 0),后续的探查地址依次为h1,h2....hm-1
(1)线性探插法
探查序列可以由下述公式得到:di=(d+i)% m
其中:di表示第i次探查的地址,m表示散列表的长度。
基本思想
将散列表T[0...m-1]看成一个循环向量,若初始探查的地址为d(即H(key)=d),则后续探查地址的序列为: d+1, d+2,..., m-1,0, 1,..., d-1。也就是说,探查时从地址d开始,首先探查T[d],然后依次探查T[d+1],...,T[m-1],此后又循环到T[0],T[1],...,T[d-1]。分两种情况分析:
- 一种运算是插入,若当前探查单元为空,则将关键字key写入空单元,若不空则继续后续地址探查,直到遇到空单元插入关键字,若探查到T[d-1]时仍未发现空单元,则插入失败(表满);
- 另一种运算是查找,若当前探查单元中的关键字值等于key,则表示查找成功,若不等,则继续后续地址探查,若遇到单元中的关键字值等于key时,查找成功,若再探查T[d-1]单元时,仍未发现关键字值等于key,则查找失败。
例
设散列函数为h(key)=key%11,散列地址表空间为0~10,对关键字序列{27,13,55,32,18,49,24,38,43),利用线性探测法解决冲突,构造散列表。并计算查找成功时的平均查找长度。
解答
【解答】首先根据散列函数计算散列地址
h(27)=5; h(13)=2; h(55)=0; h(32)=10;
h(18)=7; h(49)=5; h(24)=2; h(38)=5;
h(43)=10;
查找成功时的平均查找长度ASL= (1×5+2×2+3×1+4×1)/9≈1.78
当插入关键字49时,散列地址5已被同义词27占用,因此探查h1 = (5 + 1) % 11 = 6,此地址为开放地址,其它同理
当插入关键字38时,散列地址5已被同义词27占用,因此探查h1 = (5 + 1) % 11 = 6,也被占用,在探查h2 = (5 + 2) % 11 = 7,也被占用,继续探查探查h3 = (5 + 3) % 11 = 8,此为开放地址,将其放入
(2)二次探查法
二次探查法的探查序列为:
d0=H(K),
d1= (d0 + 12) % m
d2= (d0 - 12) % m,
d3= (d0 + 22) % m,
d4= (d0 - 22) % m,
......
hi = (H(key)±i2) % m (0≤i≤m-1)
即探查序列为:d=H(key),d+12,d-12,d+22,d-22,...等。也就是说,探查从地址d开始,先探查T[d],然后再依次探查T[d+12],T[d-12],T[d+22],T[d-22]...
(3)双重散列法
双重散列法是几种方法中最好的方法
它的探查序列为: hi= (H(key)+i * H1(key)) % m (0≤i<m-1)
即探查序列为:d=H(key), (d+1*H1 (key)) %m,(d+2*H1(key)) %m,...等。
2.拉链法(链地址法)
用拉链法处理冲突的办法是:把具有相同散列地址的关键字(同义词)值放在同一个单链表中,称为同义词链表。
有m个散列地址就有m个链表,同时用指针数组T[0..m—1]存放各个链表的头指针,凡是散列地址为i的记录都以结点方式插入到以T[i]为指针的单链表中。T中各分量的初值应为空指针。
例
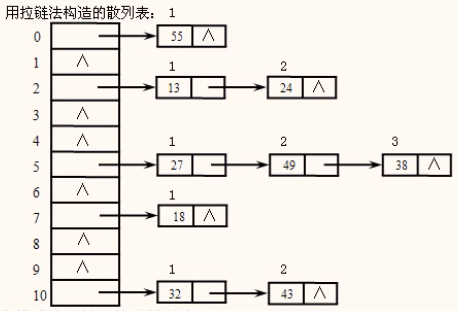
设散列函数为h (key) = key % 11;对关键字序列{27,13,55,32,18,49,24,38,43},用拉链法构造散列表,并计算查找成功时的平均查找长度。
解答
【解答】首先根据散列函数计算散列地址
h(27)=5; h(13)=2; h(55)=0; h(32)=10;
h(18)=7; h(49)=5; h(24)=2; h(38)=5;
h(43)=10;
查找成功时的平均查找长度ASL=(1×5+2×3+3×1)/9≈1.55
线性探测法平均查找长度ASL=(1x5+2x2+3x1+4x1)/9≈1.78
散列表的查找
散列表的查找过程与建表的过程基本一致。给定一个关键字值K,根据建表时设定的散列函数求得散列地址,若表中该地址对应的空间是空的,则说明查找不成功;否则,将该地址单元的关键字值与K比较。若相等则表明查找成功,否则再根据建表时解决冲突的方法寻找下一个地址,反复进行,直到查找成功或找到某个存储单元为空(查找不成功)为止。
1.线性探查法解决冲突的查找和插入算法
采用并放定值法构造散列表的类型定义:
# define M 997 //M定义为表长,一般M为一个素数
typedef struct //定义散列表结点类型
{
keyType key;
DataType data;
}NodeType;
typedef NodeType HashTable[M]; //散列表类型
假设其散列函数采用除余法,定义为:
int h(KeyType K,int m) {
//用除余法定义散列函数
return K % m;
}
(1)采用线性探查法的散列表查找算法
int HashSearch1(HashTable HT, KeyType K, int m)
{
//在长度为m的散列表HT中查找关键字值为K的元素位置
int d,temp;
d=K%m; //计算散列地址
temp=d; //temp作为哨卡,防止进入重复循环
while(HT[d].key!=-32768) //当散列地址中的key域不为空,则循环
{
if(Hr[d].key==K)
return d; //查找成功返回其下标d
else
d=(d+1)%m; //计算下一个地址
if(d==temp)
return -1; //查找一周仍无空位置,返回-1表示失败
}
return d; //遇到空单元,查找失败
}
(2)在散列表上插入一个结点的算法
int HashInsert1(HashTable HT,NodeType s,int m)
{
//在HT表上插入一个新结点s
int d;
d=HashSearchl(HT, s.key, m); //查找插入位置
if(d==-1) //表满,不能插入
return -1;
else
{
if(HT[d].key==s.key)
return 0; //表中已有该结点!
else
//找到一个开放的地址
HT[d]=s; //插入新结点S
return 1; //插入成功
}
}
2.拉链法建立散列表上的查找和插入运算
采用拉链法的散列表类定义:
typedef struct node { //定义结点类型
KeyType key;
DataType data;
node * next;
}HTNode;
typedef HTNode * HT[M]; //定义散列表类型
(1)查找算法
HTNode * HashSearch2(HT T, KeyType K, int m)
{
//在长度为m的散列表T中查找关键字值为的元素位置
HTNode *p=T[K%m]; //取K所在链表的头指针
while(p!=NULL&&p->key!=K)
p=p->next; //顺链查找
return p; //查找成功p指向K结点的位置,不成功返回NULL
}
(2)插入算法
int HashInsert2(HT T, HTNode * s,int m){//采用头插法在T表上插入一个新结点
int d;
HTNode *p=HashSearch2(T, s->key, m); //查找表中有无待插结点
if(P!=NULL)
return 0; //说明表中已有该结点
else {
//将*s插入在相应链表的表头上
d=s->key%m;
s->next=T[d];
T[d]=s;
return 1; //说明插入成功
}
}
几种处理冲突方法的散列表的平均查找长度比较
例
设散列函数h(k)=%13,散列表地址空间为0~12,对给定的关键字序列(19,14, 01,68,20,84,27,26,50,36) 分别以拉链法和线性探查法解决冲突构造散列表,画出所构造的散列表,指出在这两个散列表中查找每一个关键字时进行比较的次数,并分析在等概率情况下查找成功和不成功时的平均查找长度以及当结点数为n=10时的顺序查找和二分查找成功与不成功的情况。
解答
首先根据散列函数计算散列地址
h(19)=6; h(14)=1; h(01)=1; h(68)=3;
h(20)=7; h(84)=6; h(27)=1; h(26)=0;
h(50)=11; h(36)=10;
(1)线性探查法解决冲突构造散列表:
查找成功的平均查找长度=(1×7+2×1+3×1+4×1)/10=1.6
在上图所示的线性探查法中,假设所查的关键字K不在散列表中,若h(K)=0,则必须依次在表T[0..5]中的关键字K或空值进行比较之后才遇到T[5]为空,即比较次数为6;若h(K)=1,则需要比较5次才能确定查找不成功。类似地,对h(K)=2,3,4,5进行分析,其比较次数分别为:4,3,2,1。若h (K)=6,7,8,9时,则类似的需要比较次数分别为:4,3,2,1;而h(K)=10,11,12时,需要比较次数分别为3,2,1次才能确定查找不成功,所以查找不成功时的平均查找长度为
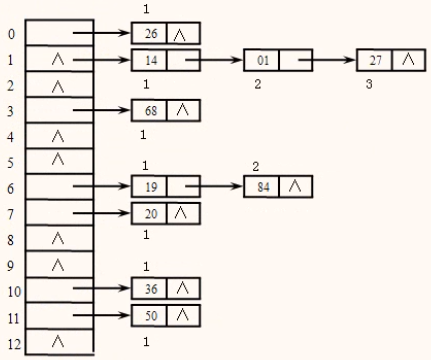
查找不成功的平均查找长度=(6+5+4+3+2+1+4+3+2+1+3+2+1)/13≈2.85(2)拉链法解决冲突构造散列表
查找成功的平均查找长度= (1×7+2×2+3×1)/10=1.4
查找不成功的平均查找长度 (不包括空指针的比较)
= (1+3+0+1+0+0+2+1+0+0+1+1+0)/13≈ 0.7
当n=10时:顺序查找成功的平均查找长度=(10+1)/2=5.5
顺序查找不成功的平均查找长度=10+1=11
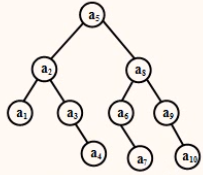
n=10的有序表的判定树:
当n=10时,二分查找成功的平均查找长度=(1×1+2×2+3×3+4×3)/10≈3
二分查找不成功的平均查找长度=(3×2+3×1+4×2+3×1+4×23×1+4×2)/11≈3.2
请注意,在计算查找成功的平均查找长度时,除数是结点的个数,而在计算查找不成功的平均查找长度时,除数却是表长。因此,同样的一组关键字对应的散列表,因表长不同,其查找成功和查找不成功时的平均查找长度都是不同的。
注意: 结点个数n,散列表长度为m。散列表的平均查找长度不是n的函数,而是装填因子
$$
α=\frac
$$
的函数,采用四种不同方法处理仲突时得出的散列表的平均查找长度;

开放定址法要求散列表的装填因子α≤1,实用中一般取0.65~0.9之间的某个值为宜。在拉链法中,其装填因子α.可以大于1,但一般均取α≤1。如:当α=0.9时,对于成功的查找,线性探查法的平均长度为5.5;二次探查法、双重散列法的平均长度是2.56;拉链法的平均长度为1.45