算法思想
插入排序(Insertion Sort)的基本思想是:每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子文件中的适当位置,直到全部记录插入完成为止。
插入排序主要包括:直接插入排序和希尔排序。
直接插入排序
排序思想
假设待排序的记录存放在数组R[1...n]中,在排序过程的某一时刻,R被划分成两个子区间,R[1...i-1]和R[i...n],其中前一个为已排好序的有序区,而后一个为无序区。
初始时,有序区只含有1个元素R[1],无序区为R[2...n]。
排序过程中,只需每次从无序区中取出第一个元素,把它插入到有序区的适当位置,使之成为新的有序区,依次这样经过n-1次插入后,无序区为空,有序区包含全部n个元素,至此排序结束
实例分析
给定一组关键字(46,39,17,23,28,55,18,46),要求按直接插入排序算法给出每一趟排序结果。
解答
排序过程如下
步骤:
temp为一个哨兵(副本),用于需要移动元素,避免元素移动时被覆盖
默认第一个元素为有序序列,放进哨兵变量
i = 1;设置temp为第一个元素46,将下标为1(39)的元素与前面元素依次进行比较,发现前面元素46比他大,往前移动,发现前面没有元素后,交换双方位置,并设置temp为当前的元素(39),结果为上图i=2
i = 2;查找下标为2(17)的元素与前面元素依次进行比较,比他大的元素往后移,直到前面没有比他大的元素,放置该元素(下标为0),temp设置为当前移动的元素(17),结果为上图i=3
i = 3;查找下标为3的元素(23),将其与前面有序区进行比较,比他大的元素往后移...直到比较完39后(39往后移),没有比他更大的元素了,则原39元素的下标就是他新的下标(2),将其放进去,temp为当前的元素(39),结果为上图i = 4
i = 4;查找下标为4的元素(28),将其与前面有序区进行比较,比他大的元素往后移...直到比较完39后(39往后移),没有比他更大的元素了,则原39元素的下标就是他新的下标(2),将其放进去,temp为当前的元素(39),结果为上图i= 5
i = 5;查找下标为5的元素(55),将其与前面有序区进行比较,发现没有比他大的元素,不动,temp为当前元素(55),结果为上图i = 6
....
直到排序结束
算法描述
/**
* 直接插入排序
* @param array 排序数组
* @param n 数组长度
**/
void InsertSort(int array[], int n)
{
//对顺序表R做直接插入排序
int i,j, temp;
temp = array[0];
for (i = 1; i < n; i++) //若R[i].key<R[i],移动
{
if (array[i] < array[i - 1]) {
temp = array[i]; //当前记录复制为哨兵
for (j = i - 1; j >= 0 && array[j] > temp; j--) //找插入位置
{
array[j + 1] = array[j]; //记录后移
}
array[j + 1] = temp; //R[i]插入到正确位置
}
}
}
算法分析
(1)哨兵的作用
算法中引进的附加记录temp称为哨兵(Sentinel),哨兵有两个作用:
- ①进入查找(插入位置)循环之前,它保存了R[i]的副本,不致于因记录后移而丢失R[i]的内容;
- ②它的主要作用是:在查拨循环中"监视"下标变量j是否越界。一旦越界(即j = 0),因为temp和自己比较,循环判定条件不成立使得查找循环结束,从而避免了在该循环内的每一次均要检测j是否越界(即省略了循环判定条件"j>=1"),使得测试查找循环条件的时间大约减少了一半。
(2)算法的时间性能分析
对于具有n个记录的文件,要进行n-1趟排序。
各种状态下的时间复杂度:
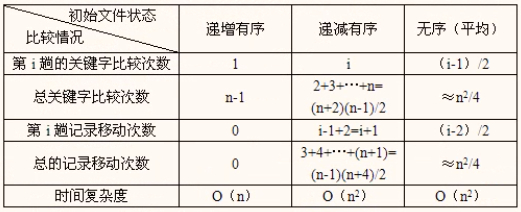
(3)算法的空间复杂度分析
算法所需的辅助空间是一个监视哨,辅助空间复杂度S(n)=O(1)。是一个就地排序。
希尔排序
排序思想
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量dt=1(dt<dt - 1<... < (d2<L),即所有记录放在同一组中进行直接插入排序为止。该方法实质上是一种分组插入方法。
简述:
- ①设置增量系列,一般按倍数递减(如下列实例,10个数,增量设置为5、3、1)
- ②将其按照增量分组(例如:首先5,中间间隔5个元素为一组),不足不分组
- 分组的元素按照直接插入排序
- ④第一个增量排序结束后,按照②③进行第二个增量排序,直至排序结束
实例分析
初始关键字序列为(36,25,48,27,65,25,43,58,76,32)。其增量序列的取值依次为5,3,1,排序过程如图所示。
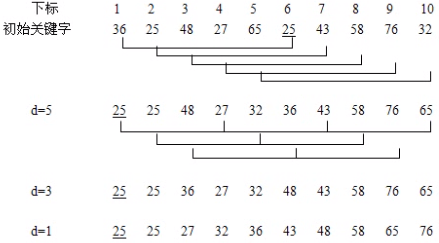
排序过程
希尔排序最重要的是增量
第一轮:增量d = 5
- 从第一个元素开始,中间间隔5个元素分组(36、25为一组),后面不足间隔5个,不分组,将其按照直接插入排序(36、25交换位置),结果为:25 25 48 27 65 36 43 58 76 32
- 第一个元素已经排过了,从第二个元素开始,中间间隔5个元素(25、43为一组)进行分组,将其排序,结果为:25 25 48 27 65 36 43 58 76 32
- 往后推,第三个元素开始,分组为48、58一组,将其排序,结果为:25 25 48 27 65 36 43 58 76 32
- 往后推,第四个元素开始,分组为27、76一组,将其排序,结果为:25 25 48 27 65 36 43 58 76 32
- 往后推,第五个元素开始,分组为65、32一组,将其排序,结果为:25 25 48 27 32 36 43 58 76 65
增量为5的已经排完(上图d = 5),进行下一轮增量排序第二轮:增量d = 3,当前序列为:25 25 48 27 32 36 43 58 76 65
- 从第一个元素开始,中间间隔3个元素分组(25、27、43、65为一组),将其按照直接插入排序,无需变动,结果为:25 25 48 27 32 36 43 58 76 65
- 从第二个元素开始,中间间隔3个元素分组(25、32、58为一组),将其按照直接插入排序,无需变动,结果为:25 25 48 27 32 36 43 58 76 65
- 从第三个元素开始,中间间隔3个元素分组(48、36、76为一组),将其按照直接插入排序,结果为:25 25 36 27 32 48 43 58 76 65
增量为3的已经排完(上图d = 3),进行下一轮增量排序...直到排序结束
算法描述
void ShellSort(int array[], int n) //希尔排序函数
{
int i, j, step;
for (step = n / 2; step > 0; step = step / 2) //这里的step是根据10个元素这种情况定义的增量
{
for (i = 0; i < step; i++) //i用来每次分割指定的增量,比如:增量为5时,第一次从下标为0开始分割5个,进行排序,下次就从下标为1开始进行分组
{
for (j = i + step; j < n; j = j + step) //数组下标j,用于每次分组的元素,如:第一次分组:0、5、10.....元素,用于排序
{
if (array[j] < array[j - step]) //比较大小,下标前面的元素是否大于下面后面的元素
{
int temp = array[j]; //将要移动的元素放到temp中
int k = j - step; //记录前一个元素下标,用于后面往前推(直接插入排序思想)
while (k >= 0 && temp < array[k]) //将要比较的元素,依次从后往前比较
{
array[k + step] = array[k]; //把大的值往后插入
k = k - step;
}
array[k + step] = temp; //把小的值往前插入
}
}
}
}
}
算法分析
(1)增量序列的选择
- ①最后一个增量必须为1;
- ②应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。
(2)Shell排序的时间性能优于直接插入排序
实验表明,当n较大时,比较和移动的次数约在n1.25到1.6n1.25之间。
(3)算法的空间复杂度分析
算法空间复杂度为O(1)。是一个就地排序。
(4)稳定性
希尔排序是不稳定的。

