基本思想
初始时将待排序序列R[1...n]看成是n个长度为1的有序序列,通过第一趟两两归并后,得到[n/2]个长度为2的有序序列,然后再两两归并,得到[n/4]个长度为4的有序序列,如此重复,直到得到一个长度为n的有序序列。这种排序成为二路归并排序
步骤
- ①将序列中待排序数组分为若干组,每n个数组分为一组(一般分为两个数组为一组)
- ②将若干个组两两合并,保证合并后的组是有序的
- ③重复第二步操作直至只剩一组,排序完成
实例分析
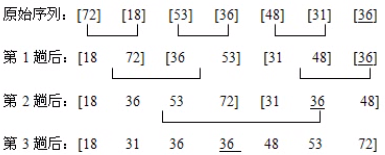
已知序列(72,18,53,36,48,31,36),请写出对该序列采用二路归并排序方法进行升序排序时各趟的结果。
过程
第一步:将待排序数组分成两两一组。如上图原始序列
第二步:将第一步分成的组进行两两合并,按从小到大排序(比如说:72与18比,18小放入新数组,然后72),合并成新的组。上图第1趟
第三步:将第二部新的组进行两两分组,按从小到大排序(拿18与72比,18小放入新数组,然后72与36比,36小放入新数组,72与53比,53小,放入,最后是72,思路是下列算法描述与),合并成新的组。上图第2趟
第四步:看还可分组不,可以的话,可以的话,进行两两分组,按从小到大排序。合并成新的分组。上图第3趟
算法描述
/*
* 归并排序
*/
/*
* 合并操作
* 将左序列的第一个数与左序列第二个数以及右序列数(因为分成两个为一组)进行逐个比较,left(right)指向的下标小于right指向的下标,
* 则将left(right)指向的数值放入新的数组temp,
* array -- 待排序数组
* left -- 左序列指针
* mid -- 中间指针
* right -- 右序列指针
* temp -- 副本数组
*/
void Merge(int array[], int left, int mid, int right, int temp[]) {
int i = left; //左序列指针
int j = mid + 1; //右序列指针
int t = 0; //临时数组指针
while (i <= mid && j <= right)
{
if (array[i] <= array[j])
{
temp[t++] = array[i++];
}
else
{
temp[t++] = array[j++];
}
}
while (i <= mid) {//将左边剩余元素填充进temp中
temp[t++] = array[i++];
}
while (j <= right) {//将右序列剩余元素填充进temp中
temp[t++] = array[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while (left <= right) {
array[left++] = temp[t++];
}
}
/*
* 递归分组,一直分组下去,直到不足够分组
* array -- 待排序的数组
* left -- 左序列指针
* right -- 右序列指针
* temp -- 副本数组
*/
void Sort(int array[], int left, int right, int temp[]) {
if (left < right)
{
int mid = (left + right) / 2;
Sort(array, left, mid, temp); //左边归并排序,使得左子序列有序
Sort(array, mid + 1, right, temp); //右边归并排序,使得右子序列有序
Merge(array, left, mid, right, temp); //将两个有序子数组合并操作
}
}
void Sort(int array[], int length) {
int temp[7];
Sort(array, 0, length - 1, temp);
}
算法分析
二路归并排序法需要进行「log2n]趟,其时间复杂度为O(nlog2n),空间复杂度为O(n)。
是一种稳定的排序方法。
