图的遍历
从某个顶点出发,沿着某条搜索路径对图中每个顶点做且仅做一次访问。
图的遍历最常用的是深度优先搜索遍历和广度忧先搜索遍历两种方法。
一.深度优先搜索遍历
思想
深度优先搜索(Depth First Search,DFS)遍历类似于树的前序(先根)遍历。递归方式
假设初始状态是图中所有顶点都未曾访问过,则可从图G中任选一顶点V为初始出发点,首先访问出发点V,并将其标记为已访问过﹔然后依次从V出发搜索V的每个邻接点W,若W未曾访问过,则以W作为新的出发点出发,继续进行深度优先遍历,直到图中所有和V有路径相通的顶点都被访问到﹔若此时图中仍有顶点未被访问,则另选一个未曾访问的顶点作为起点,重复上述过程,直到图中所有顶点都被访间到为止。
例
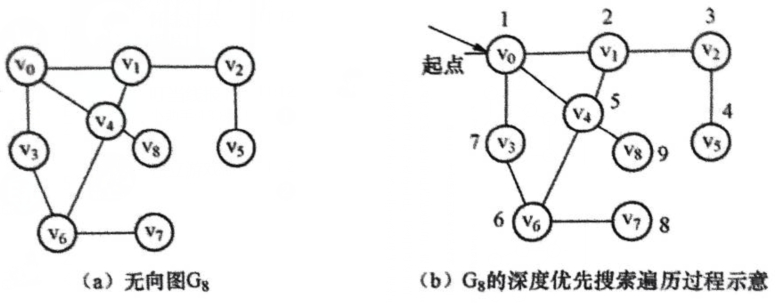
从V0开始的深度优先搜索序列:V0,V1,V2,V5,V4,V6,V3,V7,V8。
从V8开始的深度优先搜索序列:V8,V4,v0,V1,V2,V5,V3,V6,V7。
思路
假设以v0为出发点(起点)进行搜索,在访问了顶点v0之后,将其设置为真,接着选择v0的邻接点v1。
因为v1未曾访问,访问v1,再从顶点v1出发搜索,接着访问v2,访问v5
这时,顶点v5、v2的邻接点均已访问过,因此回溯到顶点v1,由于v1的邻接点v0和v2均已访问过,只有其邻接点v4未被访问,所以访问v4
v4访问完后,接着访问v6(或v8)......
直到全部访问完
假设visited[MaxVertexNum]为一全局量数组,用以标记某个顶点是否被访问过,其初值均为假值(FALSE)
1.以邻接矩阵为存储结构的深度优先搜索遍历算法
int visited[20];
void DFS(MGraph G, int i, int n)
{
//从顶点Vi出发,深度优先搜索遍历图G(邻接矩阵结构)
int j;
printf("V%d→",i); //假定访问顶点vi以输出该顶点的序号代之
visited[i]=1; //标记vi已访问过
for(j=0; j<n; j++) //依次搜索vi的每个邻接点
{
if(G.arcs[i][j]==1&&!visited[j])
DFS(G,j,n); //若(Vi,Vj)∈(G),且Vj未被访问过,则从开始递归调用
}
}
该算法的时间复杂度为O(n2)
2.以邻接表为存储结构的深度优先搜索遍历算法
int visited[20]; //全局量数组,用以标记某个顶点是否被访问过
void DFSl(ALGraph G, int i)
{
//从顶点Vi出发,深度优先搜索遍历图G(邻接表结构)
EdgeNode *p; int j;
printf("V%d→",i); //假定访问顶点vi以输出该顶点的序号代之
visited[i]=1; //标记vi已访问过
p=G[i].link; //取Vi邻接表的表头指针
while(p!=NuLL) //依次搜索vi的每个邻接点
{
j=p->adjvex; //j为vi的一个邻接点序号
if(!visited[j])
DFSl(G,j); //若(vi,vj)∈E(G),且vj未被访问过,则从开始递归调用
p=p->next; //使p指向vi的下一个邻接点
}
}
该算法的时间复杂度为O(n+e)。
二.广度优先搜索遍历
思想
广度优先搜索(BFS)遍历类似于树的按层次遍历。
其基本思想是:首先访问出发点Vi,接着依次访问Vi的所有未被访问过的邻接点Vi1,Vi2,...,Vit,并均标记为已访问过,然后再按照v1,Vi2,...,Vit的次序,访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过,依次类推,直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。
例
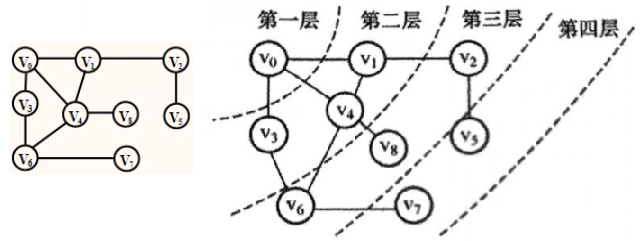
从V0开始的广度优先搜索序列:V0,V1,V3,V4,V2,V6,V8,V5,V7。
从V8开始的广度优先搜索序列:V8,V4,V0,V1,V6,V3,V2,V7,V5。
先被访问的顶点,其邻接点也先被访问,符合队列:先进先出。可以使用队列来一次记住被访问过的顶点,开始时,将v0入队列,以后每从队列中删除一个元素,就一次访问它的每一个未曾访问过的邻接点,并将其入队列。这样,当队列为空,表明所有与初始队列点相同的顶点都已访问完毕
假设visited[MaxVertexNum]为一全局量数组,用以标记某个顶点是否被访问过,其初值均为假值(FALSE)
1.以邻接矩阵为存储结构的广度优先搜索遍历算法
int visited[20];
void BFS(MGraph G,int i,int n)
{
//从顶点Vi出发,广度优先搜索遍历图G(邻接矩阵结构)
cirQueue Q; //定义一个队列
int k,j;
InitQueue(&Q); //初始化队列
printf("v%d →",i); //假定访问顶点vi用输出该顶点的序号代之
visited[i]=1; //标记Vi已访问过
EnQueue(&Q,i); //将已访问的顶点序号i入队
while(!QueueEmpty(&Q)) //当队列非空时,循环处理vi的每个邻接点
{
k=DeQueue(&Q); //册除队头元素
for(j=0; j<n; j++) //依次搜索Vk的每一个可能的
{
if(G.arcs[k][j]==1&&!visited[j])
{
printf("V%d →",j); //访问未曾访问过的顶点vj
visited[j]=1; //标记Vi已访问过
EnQueue (&Q,j); //顶点序号j入队
}
}
}
}
该算法的时间复杂度为O(n2)
2.以邻接表为存储结构的广度优先搜索遍历算法
Void BFSl(ALGraph G,int i,int n)
{
//从顶点Vi出发,广度优先搜索遍历图G
CirQueue Q; //定义一个队列指针
int j,k;
InitQueue(&Q); //初始化队列
EdgeNode *p;
int visited[20];
printf("v%d →>",i); //假定访问顶点vi以输出该顶点的序号代之
visited[i]=1; //标记vi已访问过
EnQueue(&Q,i); //将已访问的顶点序号i入队
while(!QueueErpty(&Q)) //循环处理vi的每个邻接点
{
k=DeQueue(&Q); //删除队头元素
p=G[k].link; //取vk邻接表的表头指针
while(p!=NULL) //依次搜索vk的每一个可能的邻接点
{
j=p->adjvex; //vj为vk的一个邻接点
if(!visited[j]) //若vj未被访问过
{
printf("V%d >",j); //访问未曾访问过的顶点vj
visited[j]=1; //标记vj已访问过
EnQueue (&Q,j); //顶点序号j入队
}
p=p->next; //使p指向vk邻接表的下一个邻接点
}
}
}
该算法的时间复杂度O(n+e)
注意: 由于图G=(V,E)中顶点集合V与边的集合E中元素的排列是任意的,在采用邻接表存储以后,如果存放顶点结点的先后顺序不同,或者边结点的链接次序不同,在按照某种方式遍历图时,将会影响到顶点被访问的先后顺序,即经过遍历得到的遍历序列有可能不同。即使存储结构确定,如果指定的出发顶点不同,遍历结果也会不同。当然,对于某种已经确定的存储结构与指定的出发顶点,按照某种遍历方法得到的遍历结果应该是唯一的 。
例1
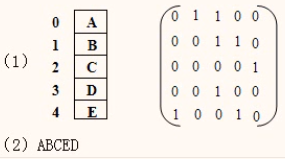
假设有如图G9,试写出该图的邻接矩阵和邻接表以及该图在邻接矩阵存储表示下从顶点v3开始搜索所得的深度优先(DFS)和广度优先(BFS)遍历序列
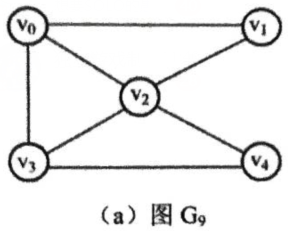
解答
(1)邻接矩阵
(2)邻接表
(3)图的深度优先搜索和广度优先搜索序列分为两种情况讨论
- 一种是在邻接矩阵表示的顺序存储结构上,遍历序列如下
- DFS的序列为:V3、v0、v1、v2、v4
- BFS的序列为:v3、v0、v2、v4、v1
- 一种是以邻接表表示的链式存储结构上,从顶点v3出发的序列如下
- DFS的序列为:v3、v4、v2、v1、v0
- BFS的序列为:v3、v4、v2、v0、v1
例2
在下图中,从顶点1出发进行深度优先遍历可得到的序列是()
A. 1 2 3 4 5 6 7
B. 1 4 2 6 3 7 5
C. 1 4 2 5 3 6 7
D. 1 2 4 6 5 3 7
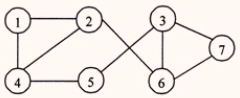
解答
【答案】B
【解析】从顶点1出发进行深度优先遍历:先访问1,然后可以访问2,接下来不可能访问3,(所以选项A错误),可以访问4,接下来可以5,不可能访问6,(所以选项D错误)。先访问1,然后可以访问4,再访问2,接下来可以6,不可能访问5,(所以选项C错误)。选项B:1 4 2 6 3 7 5 是从顶点1出发进行深度优先遍历可得到的序列。
例3
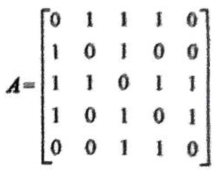
已知含6个顶点(V0,V1,v2,V3,V4,V5)的无向图的邻接矩阵如图所示,则从顶点V0出发进行深度优先遍历可能得到的顶点访问序列为()
A. (V0,V1,V2,V5,V4,V3)
B. (V0,v1,V2,V3,V4,V5)
C. (v0,V1,v5,V2,V3,V4)
D. (v0,v1,v4,V5,v2,V3)
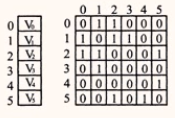
解答
【答案】A
【解析】根据给出邻接矩阵,从顶点V0出发进行深度优先遍历序列只能是:(V0,V1, V2,V5,V4,V3)
例4
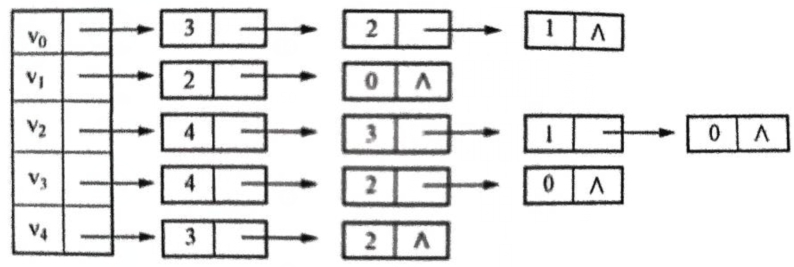
已知有向图的邻接表如图所示,请回答下面问题:
(1)给出该图的邻接矩阵;
(2)从结点A出发,写出该图的深度优先遍历序列。
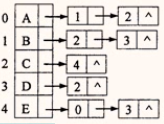
解答
【解析】由邻接表很容易给出该图的邻接矩阵﹔给出邻接表,从结点A出发,写出该图的深度优先遍历序列是唯一的。
【答案】