01月
11

发表于 • 字数统计 3431 • 被 1,431 人看爆

介绍

用来描述大小和方向两个属性的物理量

向量加减

向量的加法(减法)为各分量分别相加(相减)。可以用在计算两个力的合力或者几个速度分量的叠加，计算一个点到另一个点的位移或距离。
简单来说：求距离用向量减法，求位置移动用向量加法

向量相加

从起点指向终点的向量，比如a<0,0,0> + b<1,2,3> = c<1,2,3> 方向从a->b
如：物体移动等

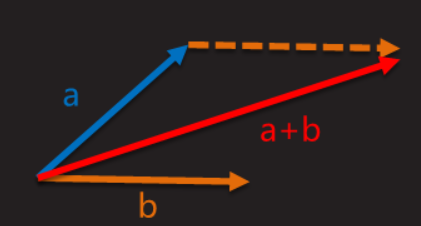
Vector01.png

向量相减

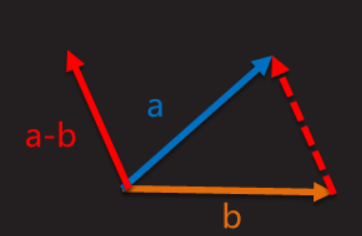
向量的减法是从终点指向起点的向量，比如a<0,0,0> - b<1,2,3> = c<-1,-2,-3> 方向从b->a
如：求距离等
几何意义：向量a与向量b相减，结果理解为以b的终点为始点，以a的终点为终点的向量，方向由b指向a

Vector02.png

向量数乘

向量与一个标量相乘称为数乘。数乘可以对向量的长度进行缩放，如果标量大于0，那么向量的方向不变，若标量小于0，则向量的方向会变为反方向。

向量点乘

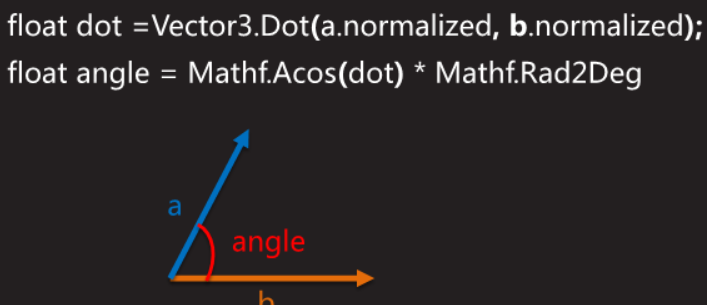
两个向量点乘得到一个标量，数值等于两个向量长度相乘后再乘以二者夹角的余弦cos
如：求两向量得到夹角 θ = arccos(a·b)
几何解释：一般来说，点乘结果描述了两个向量的“相似”程度，点乘结果越大，两个向量越相近。当两个单位向量的长度都是1的时候，向量的点乘就是他们夹角的余弦值

Vector03.png
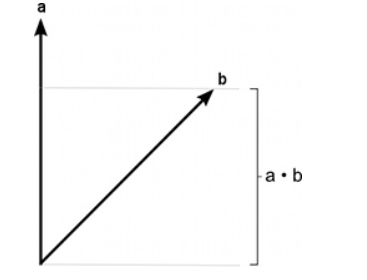
Vector05.png

例子

Vector04.png

    //playerPosition 为自己
    //enemyPosition  为敌人
    // 计算两个向量的点乘
    // 如果大于0说明敌人在自身前面
    // 如果小于0说明敌人在自身后面
    // 如果等于0说明敌人在自身左右
    Vector3 relativePosition = enemyPosition.position - playerPosition.position;    //向量减法
    Vector3 playerForward = playerPosition.forward;
    float result = Vector3.Dot(playerForward, relativePosition);
    Debug.Log(result);
    // 得到两个向量后，可以直接计算其夹角
    float angle = Vector3.Angle(playerForward, relativePosition);
    Debug.Log("两个向量的夹角：" + angle);

    // 这是前面说到的当两个向量的长度都为1时，点乘的结果就是夹角的余弦值
    float cos = Vector3.Dot(playerForward.normalized, relativePosition.normalized);
    Debug.Log("余弦值：" + cos);

    // 通过反余弦函数得到两个向量的角度
    // 不过这里得到是弧度值，并不是角度值
    float radians = Mathf.Acos(cos);
    Debug.Log("通过余弦值求弧度：" + radians);

    // 弧度值通过数据库转换成角度值
    angle = radians * Mathf.Rad2Deg;
    Debug.Log("把弧度转换成角度：" + angle);

叉乘

两个向量的叉乘得到一个新的向量，新向量垂直于原来的两个向量，并且长度等于原向量长度相乘夹角的余弦值
如：如果想得到垂直于两个向量所组成的平面的向量，就要用叉乘。判断两个向量的相对位置。叉乘方法：Vector3.Cross(a,b)
点乘判断角度，叉乘判断方向。

Vector06.png

未完待续....

参考

分享到：