按位与运算符(&)
参加运算的两个数,按二进制位进行“与”运算。
运算规则
只有两个数的二进制同时为1,结果才为1,否则为0。(负数按补码形式参加按位与运算)
即 0 & 0= 0,0 & 1= 0,1 & 0= 0,1 & 1= 1。
例题
3 &5 即 00000011 & 00000101 = 00000001 ,所以 3 & 5的值为1。
按位或运算符(|)
参加运算的两个数,按二进制位进行“或”运算。
运算规则
参加运算的两个数只要两个数中的一个为1,结果就为1。
0 | 0= 0, 1 | 0= 1,0 | 1= 1, 1 | 1= 1
例题
2 | 4 即 00000010 | 00000100 = 00000110 ,所以2 | 4的值为 6 。
异或运算符(^)
参加运算的两个数,按二进制位进行“异或”运算。
运算规则
参加运算的两个数,如果两个相应位为“异”(值不同),则该位结果为1,否则为0。
即 0 ^ 0=0,0 ^ 1= 1,1 ^ 0= 1,1 ^ 1= 0
例题
2 ^ 4 即 00000010 ^ 00000100 =00000110 ,所以 2 ^ 4 的值为6 。
按位取反运算符(~)
加运算的一个数据,按二进制进行"取反"运算。
运算规则
对一个二进制数按位取反,即将0变1,1变0。
~1=0,~0=1
正数:将数字转换成二进制后取反,然后在二进制符号位之后再次取反后加1得到最终结果二进制值,最后转换成十进制值;
负数:将数字转换成二进制后取反,然后在二进制符号位之后先加1再次取反得到最终结果二进制值,最后转换成十进制值
例题
~5---->00000101 ---->取反---->11111010 -----> 符号位后取反---->10000101---->符号位后面加1---->10000110 转换成十进制之后就是-6 , 所以~5的结果为-6
~-5---->10000101 ---->取反---->01111010---->符号位后面加1---->01111011 -----> 符号位后取反---->00000100 转换成十进制之后就是4 , 所以~-5的结果为4
左移运算符(<<)
将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)。
运算规则
设 a=1010 1110,a = a<< 2 将a的二进制位左移2位、右补0,即得a=1011 1000。
若左移时舍弃的高位不包含1,则每左移一位,相当于该数乘以2。
例题
11 << 1 -> 0000 1011 -> 0001 0110 -> 22
左移几位,就是在原数乘2^n次方
左移1位:11 * 21 = 22
左移2位:11 * 22 = 44
右移运算符(>>)
将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃。
运算规则
设 a=1010 1110,a = a >> 2 将a的二进制位右移2位、左补0,即得a=0010 1011。
操作数每右移一位,相当于该数除以2
例题
11 >> 1 -> 0000 1011 -> 0000 0101 -> 5
二进制加法
对于二进制加法和十进制的加法本质上是一样的,只是前者逢2进1,后者逢10进1。
十进制加法
1 + 1 = 2
2 + 4 = 4
二进制加法四种情况
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 //1 + 1 十进制为2,将其转化为二进制为10
例1
1 + 1 = 10 //十进制为2,将其转化为二进制为10
10 + 10 = 100 //1 + 1 二进制为10,后面0 + 0 为0,所以二进制为100
100 + 100 = 1000 //1 + 1 二进制为10,后面的0 + 0 为 0, 所以二进制为1000
1000 + 1000 = 10000 //二进制10000
10000 + 1000 = 11000 //按加法从右到左依次对应,二进制为11000
//10000 + 1000示例
10000
+ 1000
11000
例2
0111 + 1110
0111
+ 1110
10101
//从右到左进行加法
- 第一位:1 + 0 = 1
- 第二位:1 + 1 = 10,向前以为进一
- 第三位:1 + 1 = 10,刚刚第二位有进一,所以 10 + 1 = 11,向前进一
- 第四位:0 + 1 = 1,第三位有进一,所以1 + 1 = 10,前面没数字了,不需要进一
- 最终结果为10101
二进制减法
对于二进制减法和十进制的减法本质上是一样的,只是前者不足向下一位借一,然后该数加2。
减法运算可以通过将减数取反,并加1来转化为加法运算
二进制减法四种情况
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
10 - 1 = 1 //0 - 1 不足,向前借一位,然后加上该数 + 2,实际就是 2 - 1 = 1
例1
101001 - 011010 =
101001
- 011010
001111
//从右到左进行减法
- 第一位:1 - 0 = 1
- 第二位:0 - 1 不足,向前借一,然后 + 2,即 2 - 1 = 1
- 第三位:由于第二位借一,导致变为-1,需向前借一,即2 + (-1) = 1,结果1 - 0 = 1
- 第四位,第三位借一,为0,不足,向前借一,为2 + 0 = 2,即 2 - 1 = 1
- 第五位:第四位借一,为-1,不足,向前借一,为2 + (-1) = 1,即结果为1 - 1 = 0
- 第六位:由于第五位借一,变为0,即结果为:0 - 0 = 0
例2
减法运算可以通过将减数取反,并加1来转化为加法运算,比如:小的数 - 大的数。
001001 - 011010 =
001001
- 011010
- 步骤一:将减数取反,得到其反码:011010 -> 100101
- 步骤二:将反码加1,得到减数的补码:100101 + 1 = 100110
- 步骤三:将被减数和减数的补码相加:001001 + 100110 = 101111
- 步骤四:检查结果的最高位,如果是1,则表示结果为负数。根据补码表示法,负数的补码等于其原码取反再加1。所以,结果101111转化为负数形式为: -010001。因此,001001 - 011010 的结果为 -010001,即负17。
二进制乘法
和十进制乘法没什么区别,只不过在加法部分按二进制加法计算
二进制乘法四种情况
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1
例
1001 * 1101 =
1001
* 1101
------------ //先按十进制进行乘法计算
1001
0000
1001
1001
------------ //按二进制加法进行计算
1110101
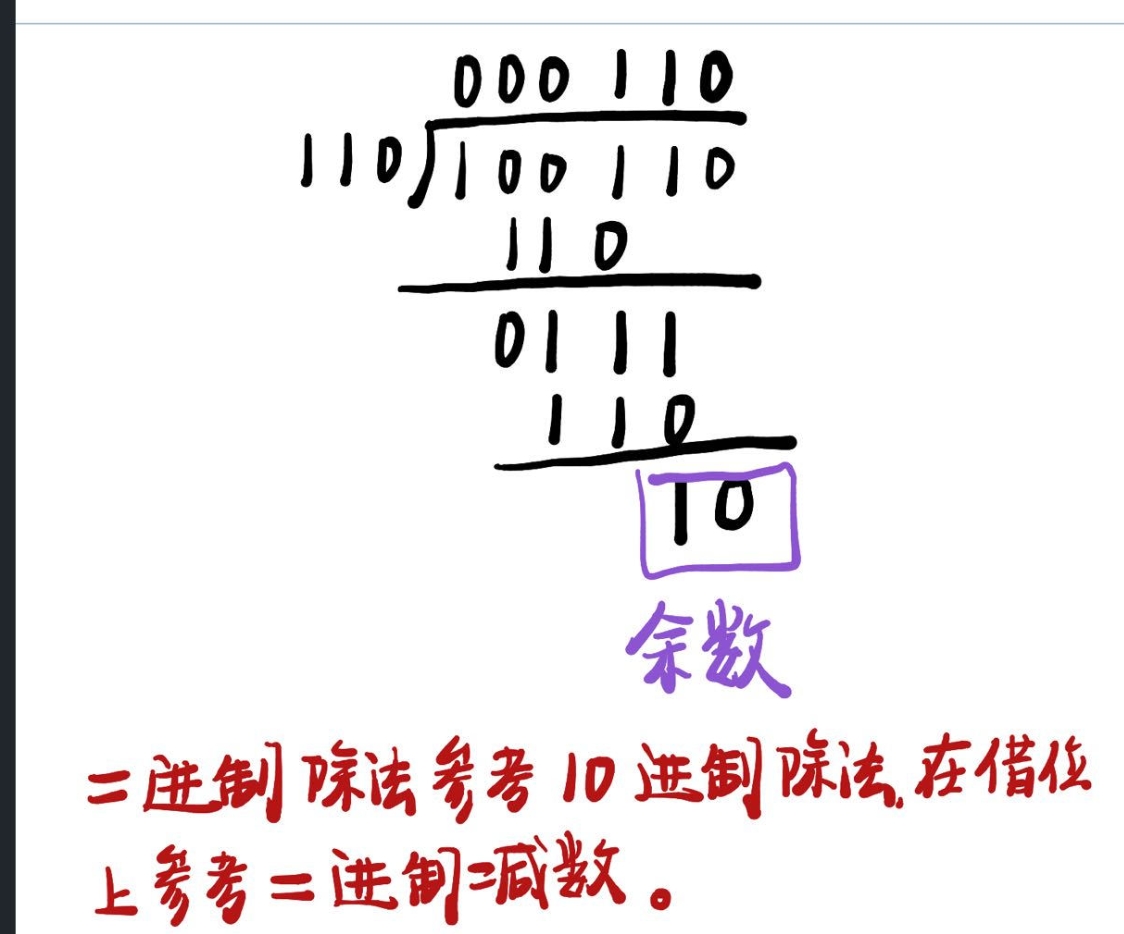
二进制除法
和十进制除法没什么区别,只不过在减法部分按二进制减法计算
二进制除法四种情况
0 / 0 = 0
0 / 1 = 0
1 / 0 = 0 (无意义)
1 / 1 = 1
例