树表定义
树表查找是对树形存储结构所做的查找
树形存储结构是一种多链表,表中的每个结点包含有一个数据域和多个指针域,每个指针域指向一个后继结点
树形存储结构和树形逻辑结构是完全对应的,都表示一个树形图,只是存储结构中的链指针代替逻辑结构中的抽象指针
因此树形存储结构(即树表)和树形逻辑结构(树)统称为树结构或树
二叉排序树定义
二叉排序树(Binary Sort Tree,BST) 又称二叉查找树,是一种特殊的二叉树,二叉排序树或者是空树,或者是满足如下性质的二叉树:
- ①若它的左子树非空,则左子树上所有结点的值均小于根结点的值;
- ②若它的右子树非空,则右子树上所有结点的值均大于根结点的值;
- ③左、右子树本身又各是一棵二叉排序树。
例
下图的就是一棵二叉排序树
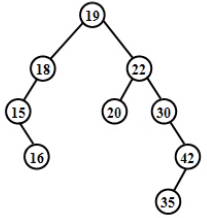
树中每个结点的关键字都大于它左子树中所有结点的关键字,而小于它右子树中所有结点的关键字,对其进行中序遍历序列:15,16,18,19,20,22,30,35,42,可见,该序列是一个有序序列
二叉排序树的重要性质
中序遍历一棵二叉排序树所得的结点访问序列是按键值的递增序列。
二叉排序树的数据类型定义
typedef struct node
{
KeyType key; //关键字
DataType other; //其他数据域
node *lchild,*rchild; //左右子树指针
} BSTNode; //结点类型
typedef BsTNode *BSTree; //二叉排序树类型
二叉排序树的插入
算法思想
在二叉排序树中插入新结点,要保证插入后仍满足BST(二叉排序树)性质。其插入过程是:
- ①若二叉排序树T为空,则为待插入的关键字key申请一个新结点,并令其为根(或新结点*S作为根结点插入到空树中);
- ②若二叉排序树T不为空,则将插入的关键字S->key和根结点关键字T->key比较:
若二者相等,则说明树中已有此关键字key,无需插入。
若S->key< T->key,则将key插入根的左子树中。
若S->key>T->key,则将它插入根的右子树中。
子树中的插入过程与上述的树中插入过程相同。如此进行下去,直到将key作为一个新的叶结点的关键字插入到二叉排序树中,或者直到发现树中已有此关键字为止。
示例分析
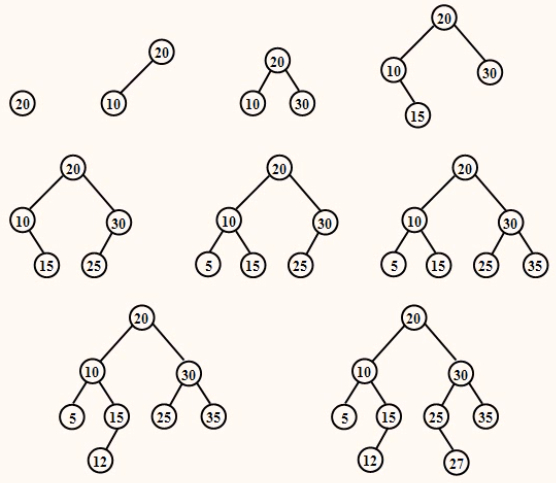
写出把无序序列(20,10,30,15,25,5,35,12,27)建成二叉排序树的过程。
解答
采用逐点插入结点的方法即可建立相应的二叉排序树。建成二叉排序树的过程如图所示
算法描述
BSTree InsertBST(BSTree T,BSTNode *S)
{
BSTNode *f,*p=T;
while(p) //找插入位置
{
f=p; //f记录p的双亲,为将来插入结点
if(S->key <p->key)
p=p->lchild;
else
p=p->rchild;
}
if(T==NULL) T=S; //T为空树,新结点作为根结点
else if(S->key <f->key)
f->lchild =S; //作为双亲的左孩子插入
else
f->rchild=S; //作为双亲的右孩子插入
return T;
}
二叉排序树的生成
算法思想
从空的二叉树开始,每输入一个结点数据,生成一个新结点,就调用一次插入算法将它插入到当前生成的二叉排序树中
算法描述
BSTree CreateBST(void)
{
//从空树开始,建立一棵二叉排序树
BSTree T=NULL; //初始化T为空树
KeyType key;
BSTNode *S;
scanf("% d",&key); //输入第一个关键字
while (key) //假设key=0是输入结束
{
S=(BSTNode *)malloc(Sizeof(BSTNode));
S->key=key; //生成新结点
S->lchild=S->rchiId=NULL;
T=InsertBST(T,S); //将新结点*S插入二叉排序树T
scanf("% d",&key); //输入下一个关键字
}
return T; //返回建立的二叉排序树
}
例1
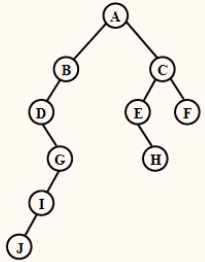
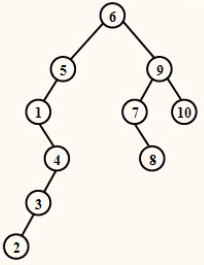
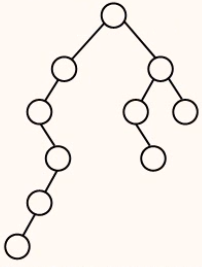
已知某二叉排序树10个结点的值依次为1~10,其结构如图所示,试标出该二叉树各结点所对应的具体值。
解答
【分析】根据二叉排序树的的特点:对二叉排序树进行中序遍历,得到的是从小到大的序列。给题中给出的二叉树各结点填入字符,如图所示﹔再对该二叉树进行中序遍历得到序列:(D,J,I,G,B,A,E,H,C,F)﹔根据二叉排序树的的特点和题目要求,这个序列对应序列(1,2,3,4,5,6,7,8,9,10)﹔将二叉树中的字符改为对应得数字即可。
【解答】二叉树各结点所对应的具体值如图所示。
例2
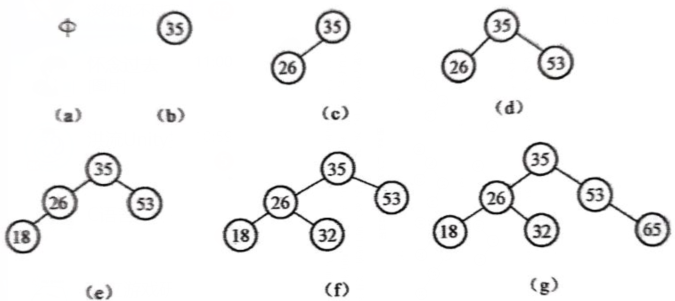
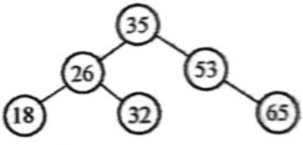
已知关键字序列为(35,26,53,18,32,65),按上述算法生成二叉排序树
解答
生成二叉排序树如下:
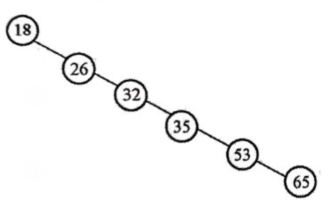
若关键字序列为(18,26,32,35,53,65),则生成的二叉排序树如下图
由二叉排序树的性质可知,在一颗非空的二叉排序树中,其结点的关键字是按照左子树、根和右子树有序的,所以对他们中序遍历得到的结点是一个有序序列
二叉排序树上的查找
算法思想
若二叉排序树为空,则表明查找失败,应返回空指针。否则,若给定值key等于根结点的关键字,则表明查找成功,返回当前根结点指针;若给定值key小于根结点的关键字,则继续在根结点的左子树中查找,若给定值key大于根结点的关键字,则继续在根结点的右子树中查找。显然,这是一个递归的查找过程
算法描述
BSTNode *SearchBST(BSTree T,KeyType x)
{
//在二叉排序树上查找关键字值为x的结点
if(T==NULL || T->key==x)
return T;
if(x<T->key)
return SearchBST(T->lchild, x);
else
return SearchBST(T->rchild, x);
算法分析
二叉排序树上的查找长度与二叉排序树的形态有关,若二叉排序树是一棵理想的平衡树(是指树中任一结点的左右子树的高度差不能大于1),则进行查找的时间复杂度为O(log2n);若退化为一棵单支树,则其查找的时间复杂度为O(n)。对于一般情况,其时间复杂度应为O(log2n)。
由此可知,在二叉排序树上查找比在线性表上进行查找的时间复杂度O(n)要好的多
例1
如下图所示二叉排序树,求平均查找长度
$ ASL = \displaystyle\sum_^6p_ic_i=(1+22+33) /6 ≈ 2.3 $
例2
如下图所示二叉排序树,求平均查找长度
$ ASL = \displaystyle\sum_^6p_ic_i=(1+2+3+4+5+6) /6 ≈ 3.5 $
例3
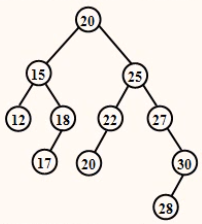
给定表(20,15,18,12,25,27,30,22,17,20,28),按数据元素在表中的次序构造一棵二叉排序树,求出其平均查找长度。
解答
按照构造二叉排序树方法,构造结果如图所示。
平均查找长度为: $ ASL = \displaystyle\sum_^6p_ic_i=(1+2×2+4×3+3×4+5×1)/11=34/11 ≈ 3.0 $
二叉排序树上的删除
从BST树上删除一个结点,仍然要保证册除后满足BST的性质。设被删除结点为p,其父结点为f,如图(a)所示的BST树。
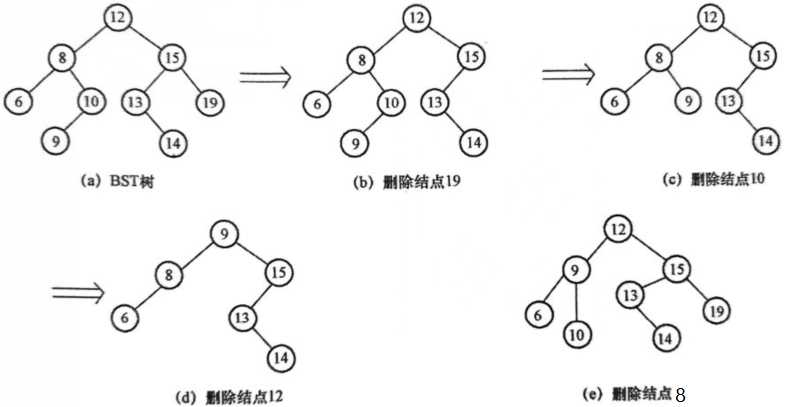
具体删除情况分析如下:
(1)若p是叶子结点:直接删除p,如图(b)所示。
(2)若p只有一棵子树(左子树或右子树),直接用p的左子树(或右子树)取代p的位置而成为f的一棵子树。即原来p是f的左子树,则p的子树成为f的左子树;原来p是f右子树,则p的子树成为f的右子树,如图(c)所示。
(3)若p既有左子树又有右子树,处理方法有以下两种,可以任选其中一种。
- ①用p的直接前驱结点(中序遍历)代替p,即从p的左子树中选择值最大的结点s放在p的位置(用结点s的内容替换结点p内容),然后删除结点s。s是p的左子树中最右边的结点且没有右子树,如图(d)所示。
- ②用p的直接后继结点(中序遍历)代替p,即从p的右子树中选择值最小的结点s放在p的位置(用结点s的内容替换结点p的内容),然后删除结点s。s是p的右子树中的最左边的结点且没有左子树。例如,对图(a)所示的二叉排序树,删除结点8后所得的结果如图(e)所示。
例
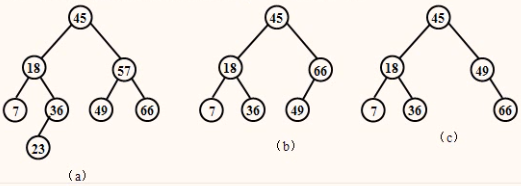
已知一棵二叉排序树如图所示。请回答下列问题:
(1)画出插入元素23后的树结构;
(2)请画出在原图中删除元素57后的树结构。
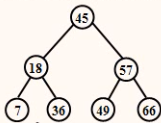
解答
(1)插入元素23后的树结构如图(a)
(2)在原图中删除元素57后的树结构如图(b)或(c)