描述
广义表是线性表的推广。即广义表中放松对表元素的原子限制,容许它们具有其自身结构。
定义
广义表是n(n≥0)个元素a1,a2,…,ai,…,an的有限序列。
其中
- ①ai--或者是原子或者是一个广义表。
- ②广义表通常记作:Ls=( al,a2,…,ai,…,an)。
- ③Ls是广义表的名字,n为它的长度。
- ④若ai是广义表,则称它为Ls的子表。
- ⑤一个表展开后所含括号的层数称为广义表的深度
注意
- ①广义表通常用圆括号括起来,用逗号分隔其中的元素。
- ②为了区分原子和广义表,书写时用大写字母表示广义表,用小写字母表示原子。
- ③若广义表Ls非空(n>1),则al是Ls的表头(head),其余元素组成的表(al,a2,…,an)称为Ls的表尾(tail)
- ④广义表是递归定义的
例如
(1)A=()--A是一个空表,其长度为零,深度为1。
(2)B=(a)--B是一个只有一个原子的广义表,其长度为1,深度为1。
(3)C=(a,(b,c))--c是一个长度为2的广义表,第一个元素是原子,第二个元素是子表,深度为2。
(4)D=(A,B,C)=((),(a),(a,(b,c)))--D是一个长度为3的广义表,其中三个元素均为子表,深度为3。
(5)E=(C,d)=((a,(b,c)),d)--E是一个长度为2的广义表,第一个元素是子表,第二个元素是原子,深度为3。
(6)F=(e,F)(e,(e,(e,...)))--F是一个递归的表,它的长度为2,第一个元素是原子,第二个元素是表自身,展开后它是一个无限的广义表,深度为∞
广义表性质
(1)广义表的元素可以是子表,而子表又可以含有子表,因此广义表是一个多层次结构的表,它可以用图来形象地表示。
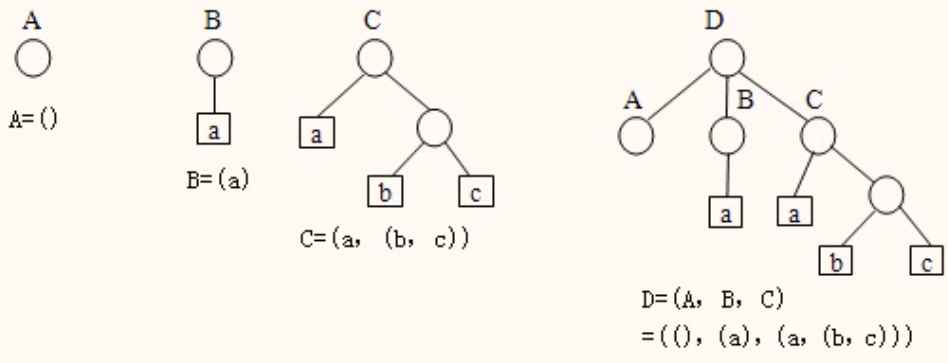
(2)广义表具有递归和共享的性质,例如,表F就是一个递归的广义表,n表是共享的表,在表D中可以不必列出子表的值,而是通过子表的名字来引用。
广义表运算
广义表的两个特殊的基本运算:取表头head(Ls)和取表尾tail(Ls)。任何一个非空的广义表其表头可能是原子,也可能是子表,而其表尾一定是子表。
例
已知有下列的广义表,试求出下面广义表的表头head()、表尾tail()、表长length()和深度depth()。
(1) A=(a,(b,c, d),e,(f,g)); (2) B=((a));
(3) C=(y,(z,w),(x,(z,w),a)); (4) D=(x,((y),B),D)。
解析
(1) head(A)=a,tail(A)=((b,c,d),e,(f,g)),length(A)=4,depth(A)=2;
(2) head(B)=(a),tail(B)=(),length(B)=1,depth(B)=2;
(3) head(C)=y,tail(C)=((z, w),(x,(z,w),a)) length(C)=3,depth(C)=3;
(4) head(D)=x,tail(D)=(((y),B),D),length(D)=3,depth(D)=∞
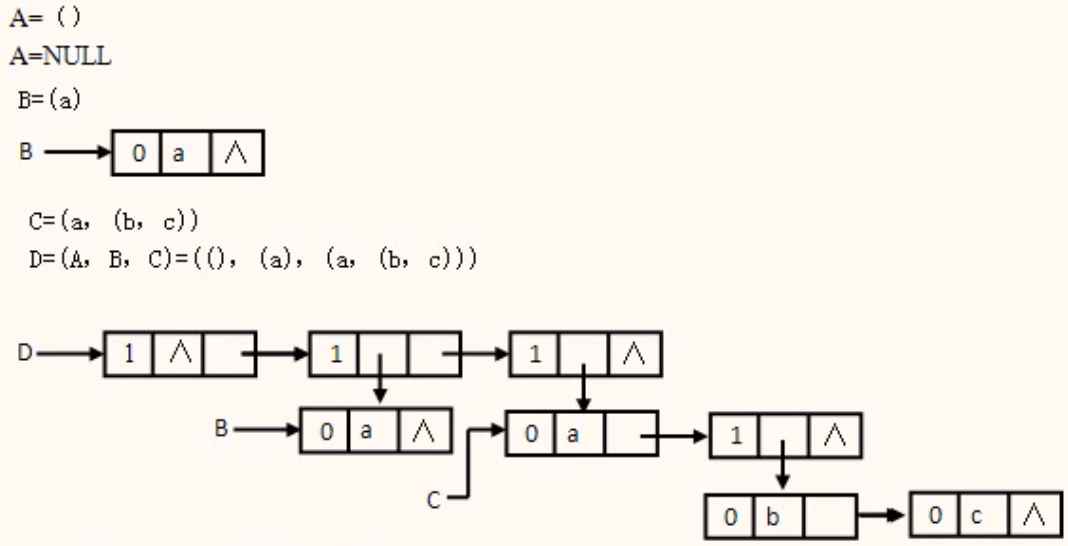
广义表的存储结构
| tag | data/slink | link |
说明:
(1) tag标志位,tag=1,该结点是子表,第二个域为slink,用以存放子表的地址,当tag=0时,该结点是原子结点,第二个域为data,用以存放元素值。
(2) link域是用来存放与本元素同一层的下一个元素对应结点的地址,当该元素是所在层的最后一个元素时,link的值为NULL。
例
以上面为例