04月
02

发表于 • 字数统计 8137 • 被 1,854 人看爆

定义

图是由顶点的非空有穷集合(用V表示该集合）与顶点之间的关系（边或弧）的集合（用E表示该集合）构成的结构。
可以形式化表示为G=(V，E)
其中，V是顶点的有限非空集合，E是由V中顶点偶对(两个顶点的连线)表示的边的集合。
V(G)表示图G的顶点集合，E(G)表示图G的边集合。
E(G)可以为空集，即图G只有顶点而没有边

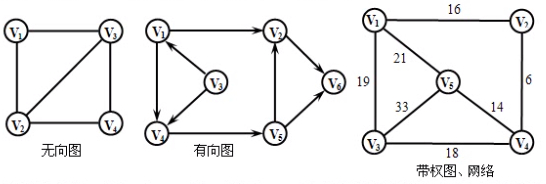
图定义.png

  对于图中任意一条边（Vi，Vj)，若(Vi，vj)是顶点的无序偶对，这样的图称为无向图。若(Vi，Vj）是顶点的有序偶对，记作<Vi，Vj>，这样的图称为有向图。直观地判断，无向图中的所有边都不带有箭头，而有向图中的所有边（习惯称之为弧）都带有箭头。Vi为入边(起始端点/起点)，Vj为出边(终止端点/终点)
  <Vi, Vj>和<Vj, Vi>是不同的有向边
  有向边又称为弧，边的起点成为弧尾，边的终点成为弧头
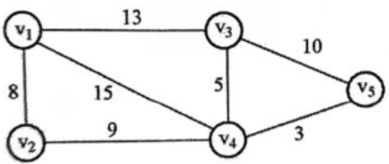
  边上带权的图称为带权图，带权的连通图称为网络 。

图的有关名词和术语

图示例.png
如图(a)所示图G1是一个有向图，该图的顶点集合和边集分别是
$V(G1) = { v1,v2,v3 } $
$E(G1) = { <v1,v2>, <v2,v3>, <v3,v1>, <v1,v3> } $

在无向图中，边均是顶点的无序对，通常用圆括号表示。因此，(vi,vj)和(vj,vi)表示同一条边
如图(b)所示G2就是一个无向图，此图的顶点集和边集分别为
$V(G2) = { v1,v2,v3,v4,v5 } $
$E(G2) = { <v1,v2>, <v1,v4>, <v2,v3>, <v2,v5>, <v3,v4>, <v3,v5>, <v4,v5> } $

边

在无向图中，若存在一条边<vi,vj>，则称顶点vi, vj为该边的两各端点，并称它们互为邻接点，或称vi和vj相邻接

在有向图中，如<vi,vj>是一条边，则称顶点vi邻接到vj，顶点vj邻接于顶点vi

用n表示图中的顶点数，用e表示图中边或弧的数目，不考虑顶点到自身的边，若(vi, vj)或<vi, vj>是E(G)的一条边，则要求vi≠vj

无向图，e的取值范围0 ~ $ \frac{1}{2} $n(n-1)，将具有$ \frac{1}{2} $n(n-1)边成为无向边
有向图，e的取值范围0 ~ n(n-1)，称具有n(n-1)边或弧的有向图成为完全图

顶点的度

  所谓某个顶点V的度是指依附于该顶点的边或弧的数量，记为D(V)。对于无向图而言，仅此而已。而对于有向图，要区分顶点的出度与入度的概念。
  所谓一个顶点V的出度是指以该顶点为出发点的孤的数量，记为OD(v)。
  所情一个顶点V的入度是指以该顶点为终止点的弧的数量，记为ID(v)。
  D (V) = OD(v) + ID(v) 。

结论：

  • ①所有顶点的度之和等于边或弧的条数2倍。
  • ②具有n个顶点的无向图中边的数目最多为n(n-1)/2，具有n个顶点的有向图中边（弧）的数目最多为n(n-1)。

例如

上图中G2中顶点v3的度D(v3) = 3；图G1中顶点v1的入度ID(v1) = 1，出度OD(v1) = 2，所以D(v1) = ID(v1) + OD(v1) = 1 + 2 = 3
图G1的边数e = (D(v1) + D(v2) + D(v3)) / 2 = (3 + 2 + 3) / 2 = 4

路径

  顶点Vx与Vy之间有路径是指存在着顶点序列Vx，Vi1，Vi2，...，Vy，并且序列中相邻两个元素构成的顶点偶对分别表示图中的一条边或弧。这里,称Vx为出发点，Vy为终止点，出发点与终止点相同的路径称为环 或 回路 。序列中顶点不重复出现的路径称为简单路径 。
  对于不带权的图，两个顶点之间的路径长度 是指该路径上所经过的边的数目。对于带权的图，两个顶点之间的路径长度是指该路径上所经过的边上的权值之和。

子图

  对于图G=(V，E)与G' = (v'，E')，若有V'⊆V,E'⊆E ，则称G'是G的一个子图。一个图是其自身的子图 。

例

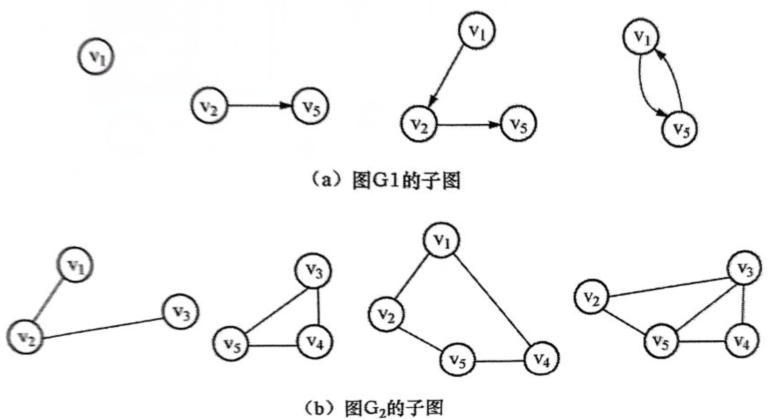
子图示例.png

图(a)中所示就是上面图(a)所示图G1的子图
图(b)中所示就是上面图(b)所示图G2的子图

图的连通

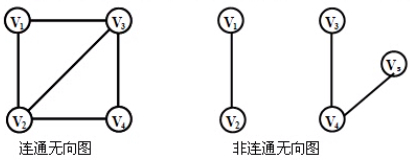
无向图的连通： 若顶点Vx与Vy之间有路径，就称Vx与Vy是连通的。若图中任意两个顶点之间都有路径，就称该无向图是连通的。

无向图的连通.png

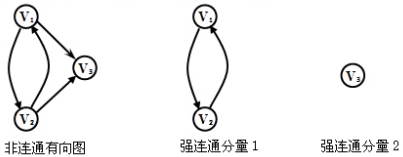
有向图的连通： 若顶点Vx与Vy之间有路径，并且顶点Vy与Vx之间也有路径，就称Vx与Vy是连通的。若图中任意两个顶点之间都有连通，就称该有向图是强连通的。

有向图的连通.png

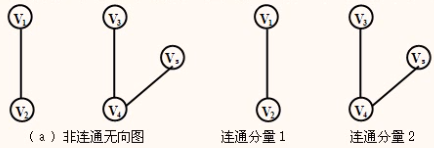
连通分量： 无向图中的极大连通子图。任何一个连通图的的连通分量只有一个，是它本身

连通分量.png

强连通图： 任意两个顶点vi和vj都连通，即从vi到vj和从vj到vi都存在路径，则称图G为强连通图
强连通分量： 有向图中的极大连通子图。

强连通分量.png

权： 一个图的每条边标上某种数值，该数值为该边的权
带权图： 边上带权的图
网络： 带权的连通图

带权图示例.png

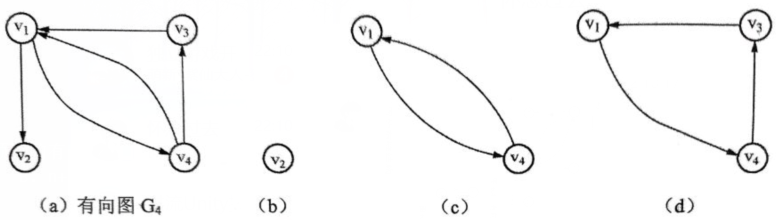
例

如下图(a)中的G4有三个强连通分量，分别对应图(b)、(c)和(d)

有向图及其强连通图.png

图的存储结构

对于具有n个顶点的图，最常采用的存储方法有邻接矩阵存储方法与邻接表存储方法。

一.邻接矩阵表示法

表示图形中顶点之间相邻关系的矩阵

设G=(V,E）是具有n个顶点的图，则G的邻接矩阵是具有如下定义的n阶方阵:

$$
A[i][j]= \left{ \begin 1 & 当(Vi, Vj)或<Vi，Vj>是E(G)的边\ 0 & 当(Vi, Vj)或<Vi，Vj>不是E(G)的边\end \right}
$$

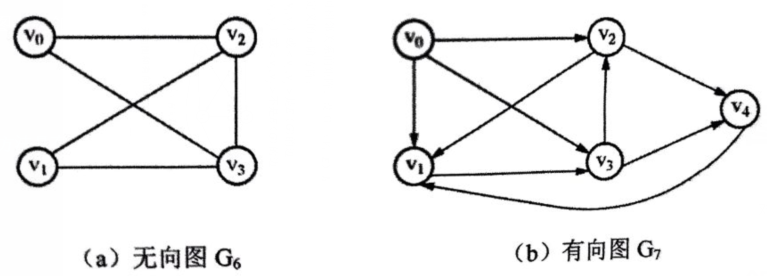
例1

下图中无向图G6和有向图G7的邻接矩阵分别对应A1和A2
邻接矩阵有无向图.png
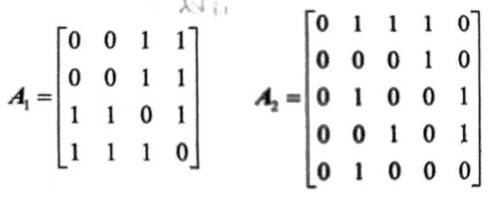
有无向图邻接矩阵.png

例2

带权的邻接矩阵
将1换为相应边上的权值，0的位置上可以不动或将其换成无穷大∞表示，如下图
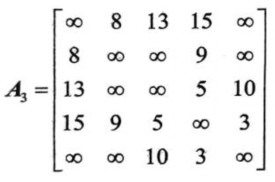
带权图的邻接矩阵.png

采用邻接矩阵存储方法具有以下特点:

  • ①无向图的邻接矩阵一定是一个对称矩阵。因此，按照压缩存储的思想，在具体存放邻接矩阵时只需存放上(或者下)三角形难的元素即可。
  • ②不带权的有向图的邻接矩阵一般来说是一个稀疏矩阵（特别是对于稀疏图)，于是可以采用三元组表的方法存储邻接矩阵。
  • ③对于无向图，邻接矩阵的第i行（或者第i列）非零元素（或者∞元素）的个数正好是第i个顶点的度D(Vi)。
  • ④对于有向图，邻接矩阵的第i行〈或者第i列)非零元素（或者非∞元素）的个数正好是第i个顶点的出度OD(Vi)(或者入度ID(Vi))。
  • ⑤对于无向图，邻接矩阵的所有非零元素（或者非∞元素）的个数正好是边数的2倍。
  • ⑥对于有向图，邻接矩阵的所有非零元素（或者非∞元素）的个数正好等于弧数。
  • ⑦一个图的邻接矩阵表示是唯一的。

邻接矩阵的存储结构

除需要一个二维数组存储顶点之间相邻关系的邻接矩阵外，还需要使用一个具有n个元素的一位数组来存储顶点信息

#define MaxVertexMum 50             //最大顶点数
typedef Struct
{
    vertexTvpe vexs[MaxVertexNum];      //顶点数组，类型假定为char型
    Adjmstrix arcs [MaxVertexNum][MaxVertexNum];        //邻接矩阵，假定为int型
}

建立一个无向网的算法

算法描述

Void createMGraph(MGraph *G，int n,int e)
{
    //采用邻接矩阵表示法构造无向网G，n、e表示图的当前顶点数和边数
    int i，j，k，w;
    scanf("%d，%d"，&n，&e);        //读入顶点数和边数
    for(i=0; i<n; i++)              //输入顶点信息
        scanf("%c"，&G->vexs[i]);
    for(i=0;i<n; i++)
    {
        for(j=0; j<n; j++)
            G->arcs[i][j]=INT_MAX;          //初始化邻接矩阵元素为无穷大，一般填32767
        for(k=0; k<e; k++)                  //读入e条边，建立邻接矩阵
        {
            scanf("%d，%d，%d"，&i，&j，&w);    //读入一条边的两端顶点序号i、j及边上的权W
            G->arcs[i][j]=w;
            G->arcs[j][i]=w;                //置矩阵对称元素权值
            
        }
    }
        
}

算法的时间复杂度O(n2)

二.邻接表表示法

邻接表

链式存储结构。类似于树的孩子链表表示法
对于具有n个顶点的图建立n个线性链表。每一个链表最前面都分别设置一个称之为顶点表结点，n个顶点构成一个数组结构。第i个链表中的每一个链结点称之为边表结点。

对于图G中每个顶点vi，把所有邻接于vi的顶点vj链成一个单链表，这个单链表称为 顶点vi的链接表

邻接表中每个表结点有两个域：
邻接点域： adjvex，用来存放与顶点vi相邻接的顶点vj的序号j
指针域： next，用来将邻接表的所有结点链在一起
数据域： 表示边上的权值

每个顶点vi的邻接表设置具有两个域的表头结点
顶点信息域： vertex
指针域： link，指向邻接表，是vi的邻接表的头指针

为了便于随机访问任一顶点的邻接表，需要把这n个表头指针用一个一维数组存储起来，这个数组(向量)就构成了图的邻接表的表示，其中第i个分量存储vi邻接表的表头指针

对于无向图，vi的邻接表中每个表结点都对应于与vi相关联的一条边
对于有向图，vi的邻接表中每个表结点都对应于以vi为起点射出的一条边
边表： 无向图的邻接表
出边表： 有向图的邻接表
顶点表： 邻接表的表头向量

无向图的邻接表
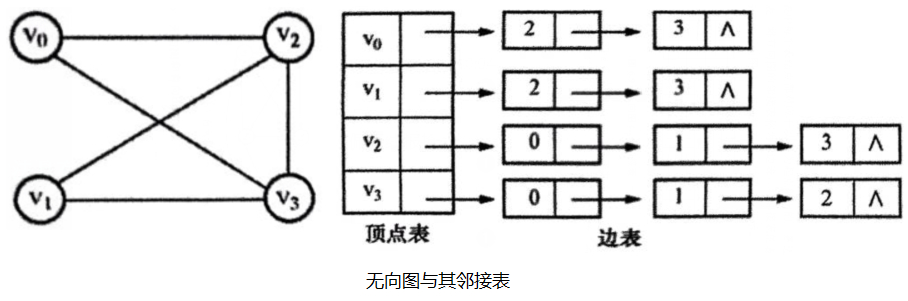
无向图与其邻接表.png

有向图的邻接表
有向图除了有一个邻接表(以vi为起点)，还需建立一个逆邻接表(入边表)，即以vi为端点的邻接表

有向图的邻接表.png

例
图的邻接表示例.png

采用邻接表存储方法具有以下特点:

  • ①一个图的邻接表表示法不唯一，这是因为邻接表中各结点的链接次序取决于建立邻接表的算法（前插法还是后插法建链表）及边的输入次序。
  • ②对于无向图，若它有n个顶点，e条边，则其邻接表中需要2e+n个结点。其中有2e个边表结点，n个顶点表结点。边表结点的个数一定是偶数，为边数的2倍。
  • ③对于有向图，若它有n个顶点，e条边，则其邻接表中需要e+n个结点。其中有e个边表结点，n个顶点表结点。
  • ④对于无向图，第i个链表中的边表结点的数目是第i个顶点的度。
  • ⑤对于有向图，第i个链表中的边表结点的数目是第i个顶点的出度。在其逆邻接表中，第i个链表中的边表结点的数目是第i个顶点的入度。
  • ⑥在所有链表中，其邻接点域值为i的结点的个数是顶点vi的入度

图的邻接表存储结构定义

#define MaxVertexNum 20
typedef char VertexType;
typedef struct node {               //边表结点类型
    int adjvexj;                    //顶点的序号
    struct node *next;              //指向下一条边的指针
}EdgeNode;

typedef struct vnode                //顶点表结点
{
    VertexType vertex;              //顶点域
    EdgeNode *link;                 //边表头指针
}VNode,Adjlist[MaxVertexNum];       //邻接表

typedef Adjlist ALGraph;            //定义为图类型

无向图邻接表的建表算法:

void CreateGraph(ALGraph GL，int n,int e)
{
    //n为顶点数，e为图的边数
    int i，j，k;EdgeNode *p;
    for(i=0; i<n; i++)              //建立顶点表
    {
        GL[i].vertex=getchar ();    //读入顶点信息
        GL[i].link=NULL;            //边表头指针置空  
    }
    
    for(k=0; k<e; k++)              //采用头插法建立每个顶点的邻接表
    {
        scanf("%d，%d"，&i，&j);    //读入边(vi，vj)的顶点序号
        p=(EdgeNode*)malloc(sizeof(EdgeNode));      //生成新的边表结点
        p->adjvex=j;                //将邻接点序号j赋给新结点的邻接点域
        p->next=GL[i].link;
        GL[i].link=p;               //将新结点插入到顶点vi的边表头部
        p=(EdgeNode*)malloc(sizeof(EdgeNode));      //生成新的边表结点
        p->adj.vex=i;               //将邻接点序号i赋给新结点的邻接点域
        p->next=GL[j].link;         
        GL[j].link=p;               //将新结点插入到顶点vj的边表头部
    }
    
}

算法的时间复杂度O(n+e)
建立有向图的邻接表更加简单，每当读入一个顶点对<i，j>时，仅需要生成一个邻接点序号为j的边表结点，将其插入到v的出边表头即可。

图下一篇-图的运算

分享到：